Popisná statistika: míry polohy (s příkazy pro Excel a jazyk R)

Zpracování popisných charakteristik patří mezi základní úkony při analýze dat. V tomto díle se zaměříme na míry polohy. Prozkoumáme, proč a jak je vůbec počítat a v jakých situacích je použít. Podívejte se i na detaily o mírách četnosti, mírách variability a mírách tvaru.

Poznámka: pro výpočet některých měr polohy a dalších popisných charakteristik v jazyce R budete potřebovat knihovny tidyverse, rstatix a psych, které nainstalujete následujícím příkazem:

# instalace knihoven
install.packages(c("tidyverse", "rstatix", "psych", "DescTools"))

Co jsou míry polohy?

Míry polohy popisují různé druhy středu datového souboru. Řadíme sem:

• modus,
• různé druhy průměrů (aritmetický, vážený, geometrický, harmonický průměr a kvadratický průměr),
• různé druhy kvantilů (včetně mediánu).

Jednotlivé míry polohy můžeme použít u následujících typů proměnných:

Pro další analýzu je to zcela zásadní informace, protože podle typu rozložení (distribuce) hodnot sledované proměnné můžeme zvolit takový statistický test, který nám pomůže (ne)vyvrátit naši vědeckou hypotézu.

Zvýhodněné balíčky kurzů

Zakupte si balíček 2 nebo více vybraných kurzů a ušetřete

Prohlédnout balíčky kurzů

U normálního rozložení pravděpodobnosti (Gaussovy křivky) dosahuje nejvyšší počet naměřených hodnot středu histogramu (viz níže). Modus, medián i průměr nabývají totožné hodnoty:

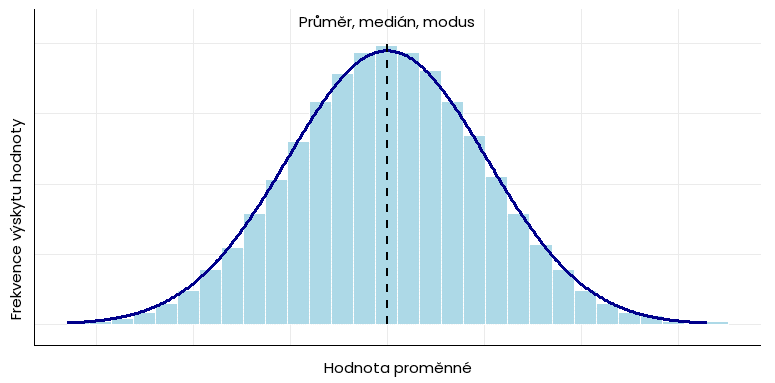
V případě jiného než normálního rozdělení dat, kdy se nejvyšší počet naměřených hodnot nalézá mimo střed histogramu, mají modus, medián a průměr odlišné hodnoty:

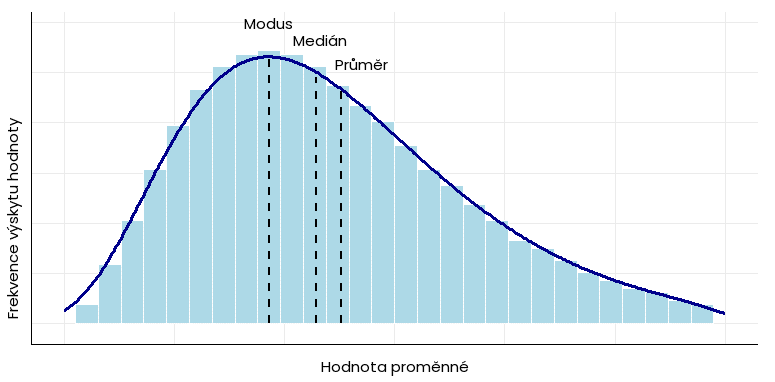
Modus

Modus je nejčastější hodnota (frekvence výskytu) zkoumané proměnné (statistického znaku), např.:

• nominální data – nejčastější vedlejší účinek u experimentálního léku na gliom,
• ordinální data – nejčastější stádium gliomu, se kterým pacienti přicházejí k lékaři,
• diskrétní proměnné – nejčastější počet léčebných cyklů podaný pacientovi,
• spojité proměnné – nejčastější koncentrace experimentálního léku v krvi hodinu po podání.

Výhody: modus neovlivňují extrémní hodnoty

Nevýhody: u malých vzorků není modus dostatečně reprezentativní

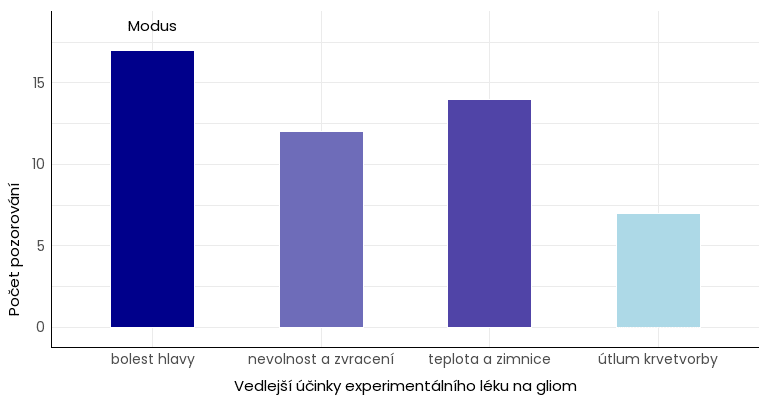
Příklad modu u nominální proměnné.

Příklad modu u spojité proměnné, která nabývá v určitém rozsahu libovolných hodnot – pro účely vizualizace se proto zobrazuje počet hodnot v rámci určitých intervalů.

Excel: funkce pro výpočet modu

V Excelu můžete pro nalezení modu použít dvě funkce:

• Funkce MODE je vhodná v situaci, kdy soubor hodnot obsahuje pouze jeden modus; v opačném případě vrátí pouze první nalezený modus.
• Funkce MODE.MULT vrátí všechny nalezené mody; je tedy ideální pro situace, kdy počet očekávaný modů neznáte nebo jich očekáváte více.

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet prvního modu
=MODE(A1:A100)

# funkce pro výpočet všech modů
=MODE.MULT(A1:A100)

R: kód pro výpočet modu

Pro nalezení modu v jazyce R můžete využít tyto funkce:

• get_mode z balíčku rstatix vrátí hodnoty všech modů,
• Mode z balíčku DescTools vrátí 1) hodnoty všech modů, 2) početní zastoupení těchto hodnot.

# načtení knihoven
library(rstatix)
library(DescTools)

# naměřené hodnoty
data <- c("Male", "Female", "Female", "Female", "Male")

# funkce pro výpočet modu
get_mode(data)

# funkce pro výpočet modu a početního zastoupení modu
Mode(data)

Průměr

Průměr zachycuje středovou hodnotu zkoumané proměnné. Podle povahy statistického znaku rozlišujeme:

Aritmetický průměr

Aritmetický průměr, jeden z nejvyužívanějších statistických ukazatelů, vyjadřuje střední hodnotu datové sady. Počítá se jako součet všech hodnot proměnné dělený celkovým počtem hodnot.

Je základem pro výpočet rozptylu a směrodatné odchylky.

Nevýhody: velká citlivost na odlehlé hodnoty, které mohou významně zkreslit celkový pohled na datový soubor. Odlehlé hodnoty mohou poukazovat na chybu v měření či výběru vzorku, může jít ale také o skutečnou hodnotu, která se od ostatních výrazně liší (na téma odlehlých hodnot pro vás připravujeme samostatný článek).

Zobrazit postup výpočtu aritmetického průměru >

Excel: funkce pro výpočet aritmetického průměru

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet aritmetického průměru
=AVERAGE(A1:A100)

R: kód pro výpočet aritmetického průměru

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet aritmetického průměru
mean(data)

Vážený průměr

Váženým průměrem počítáme střední hodnotu v datové sadě, ve které má každá hodnotu přiřazenou určitou váhu (např. při zkoumání léku na úzkostnou poruchu budeme výsledkům u jedinců se silnou úzkostí přiřazovat vyšší váhu).

Využijete jej také pro analýzu různé velkých skupin (např. výpočet celkové průměru u žáků z malé a velké školy).

Výhody: při správném nastavení vah poskytuje přesnější informace o střední hodnotě než aritmetický průměr.

Nevýhody: v určitých situacích obtížné nastavení vah a z toho vyplývající nepřesný výsledek. (Např. při hodnocení účinnosti různých vzdělávacích metod může být obtížné určit váhu vlivu učebních materiálů, metody výuky a kvalifikace učitelů.)

Zobrazit postup výpočtu váženého průměru >

Excel: funkce pro výpočet váženého průměru

# buňky A1 až A100 obsahují naměřené hodnoty
# buňky B1 až B100 obsahují váhy jednotlivých hodnoty

# funkce pro výpočet váženého průměru
=SUMPRODUCT(A1:A100, B1:B100) / SUM(B1:B100)

R: kód pro výpočet váženého průměru

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# váhy naměřených hodnot
weights <- c(0.1, 0.3, 0.3, 0.2, 0.1)

# funkce pro výpočet váženého průměru
weighted.mean(x=data, w=weights)

Geometrický průměr

Geometrický průměr používáme pro výpočet střední hodnoty u proměnných, které vykazují zřetězené růstové charakteristiky (počítáme tedy jejich průměrné tempo růstu či poklesu – např. u bakteriálních kolonií, populace či HDP).

Výhody: menší citlivost na odlehlé hodnoty než aritmetický průměr.

Nevýhody: nelze použít pro nulové a záporné hodnoty.

Zobrazit postup výpočtu geometrického průměru >

Excel: funkce pro výpočet geometrického průměru

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet geometrického průměru
=GEOMEAN(A1:A100)

R: kód pro výpočet geometrického průměru

# načtení knihovny
library(psych)

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet geometrického průměru
geometric.mean(data)

Harmonický průměr

Harmonický průměr využijete při výpočtu střední hodnoty u proměnných, které mají charakter podílu, resp. převrácené hodnoty – jde např. o:

• jednotky jako rychlost (podíl vzdálenosti k času),
• účinnost (podíl užitečného výstupu ke vstupu),
• celkový elektrický odpor (součet převrácených hodnot jednotlivých odporů),
• koncentraci látky v roztoku (hmotnost sloučeniny ku objemu roztoku).

Výhody: díky využití převrácených hodnot má harmonický průměr mnohem menší citlivost na odlehlé hodnoty než aritmetický průměr.

Nevýhody: nelze použít pro nulové a záporné hodnoty.

Zobrazit postup výpočtu harmonického průměru >

Excel: funkce pro výpočet harmonického průměru

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet harmonického průměru
=HARMEAN(A1:A100)

R: kód pro výpočet harmonického průměru

# načtení knihovny
library(psych)

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet harmonického průměru
harmonic.mean(data)

Medián a další kvantily

Kvantilem označujeme ukazatel, která rozděluje získaná data na určité procentní podíly. Pod hodnotou daného kvantilu tedy leží specifikované procento všech pozorování – např. kvantil Q0,4 označuje místo, pod kterým leží prvních 40 % naměřených hodnot (v zásadě jde tedy o definici percentilu, viz níže).

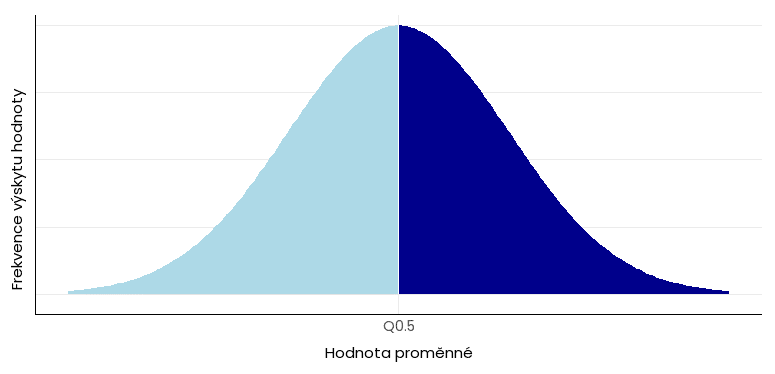
Medián

Medián je kvantil, který dělí získané hodnoty na dvě poloviny (Q). Označuje se jako Q0,5. Pro lichý a sudý počet hodnot se počítá odlišně:

Výhody: méně citlivý na odlehlé hodnoty než průměr.

Nevýhody: citlivý na chybějící data (při výpočtu bere v potaz pořadí hodnot); u velkých souborů hodnot obtížný výpočet (náročné na výkon procesoru).

Zobrazit postup výpočtu mediánu >

Excel: funkce pro výpočet mediánu

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet mediánu
=MEDIAN(A1:A100)

R: kód pro výpočet mediánu

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet mediánu
median(data)

Kvartil

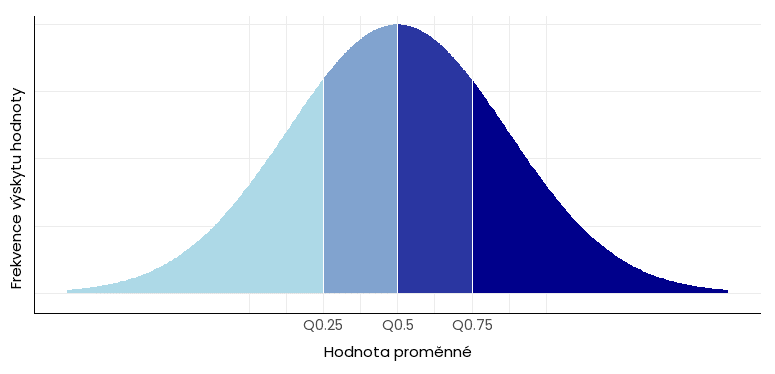
Kvartil je typ kvantilu, který rozděluje datovou sadu na čtyři stejně velké části. Existují tři kvartily, které se obvykle označují jako Q1 (resp. 0,25), Q2 (resp. Q0,5) a Q3 (resp. Q0,75).

Hodnoty Q0,25 a Q0,75 se často používají k identifikaci odlehlých dat – jde o hodnoty, které leží mimo rozpětí těchto kvartilů (tzv. mezikvartilové rozpětí; viz krabicový graf níže).

Kvartily se počítají podle následujícího vzorce:

\( Q_k \) označuje pořadí hodnoty k-tého kvartilu v souboru vzestupně seřazených dat (k = 1 pro první kvartil, k = 2 pro medián a k = 3 pro třetí kvartil). Proměnná \( n \) vyjadřuje počet hodnot v datovém souboru.

Výhody: méně citlivý na odlehlé hodnoty než průměr; přináší více informací než medián.

Nevýhody: kvůli rozdělení jen do čtyř skupin mohou kvartily skrývat detaily o rozložení dat.

Zobrazit postup výpočtu kvartilů >

Excel: funkce pro výpočet kvartilů

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet kvartilů
=QUARTILE(A1:A100, 1)  # pro výpočet Q0,25
=QUARTILE(A1:A100, 2)  # pro výpočet Q0,5 (medián)
=QUARTILE(A1:A100, 3)  # pro výpočet Q0,75

R: kód pro výpočet kvartilů

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet kvartilů
quantile(data, probs = c(0.25, 0.50, 0.75))

Kvintil

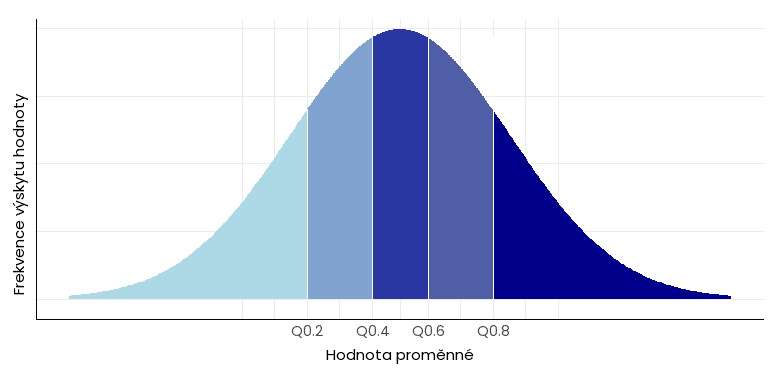
Kvintil je typ kvantilu, který rozděluje datovou sadu na pět stejně velkých segmentů. Existují čtyři kvintily, označované jako Q0,2, Q0,4, Q0,6 a Q0,8, resp. jako Q1, Q2, Q3 a Q4 (pozor, toto označení má jiný význam než u kvartilů).

Kvintily se počítají podle následujícího vzorce:

\(Q_k \) označuje pořadí hodnoty k-tého kvintilu v souboru vzestupně seřazených dat (k = 1 pro první kvintil, k = 2 pro druhý kvintil, k = 3 pro třetí kvintil a k = 4 pro čtvrtý kvintil). \(n \) je počet hodnot v datovém souboru. V praxi kvintily počítáme s pomocí statistických programů.

Výhody: méně citlivé na odlehlé hodnoty než průměr. Dávají přesnější pohled na rozdělení dat než kvartily.

Nevýhody: neobsahují hodnotu mediánu, kvůli rozdělení pouze do pěti skupin mohou kvintily skrývat detaily o rozložení dat.

Zobrazit postup výpočtu kvintilů >

Excel: funkce pro výpočet kvintilů

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet kvintilů
=PERCENTILE.INC(A1:A100, 0.2)  # pro výpočet Q0,2
=PERCENTILE.INC(A1:A100, 0.4)  # pro výpočet Q0,4
=PERCENTILE.INC(A1:A100, 0.6)  # pro výpočet Q0,6
=PERCENTILE.INC(A1:A100, 0.8)  # pro výpočet Q0,8

R: kód pro výpočet kvintilů

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet kvintilů
quantile(data, probs = c(0.2, 0.4, 0.6, 0.8))

Percentil

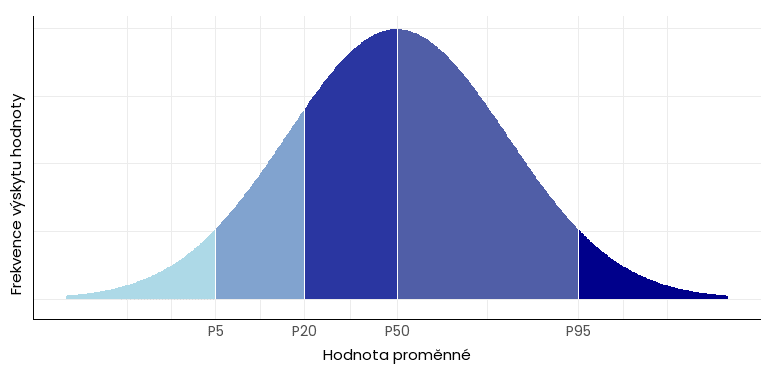
Percentil je kvantil, který ukazuje celočíselný podíl (procento) pozorovaní v datové sadě pod určitou hodnotou. Např. 30. percentil (označovaný jako P30) je hodnota, pod kterou leží 30 % všech pozorování.

Percentily se počítají podle tohoto vzorce:

\(P_k \) označuje pořadí hodnoty k-tého percentilu v souboru vzestupně seřazených dat. \(n \) je počet hodnot v datovém souboru. V praxi se percentily počítáme s pomocí statistických programů.

Ve zdravotnictví a dalších oblastech se percentil mj. využívá pro stanovení norem a standardů (viz graf níže).

Výhody: méně citlivý na odlehlé hodnoty než průměr; umožňuje zobrazit detailní rozložení dat.

Nevýhody: při malé datové sadě nemusí být hodnota vypočítaných percentilů dostatečně přesná (zejména s ohledem na extrémní hodnoty).

Zobrazit postup výpočtu percentilů >

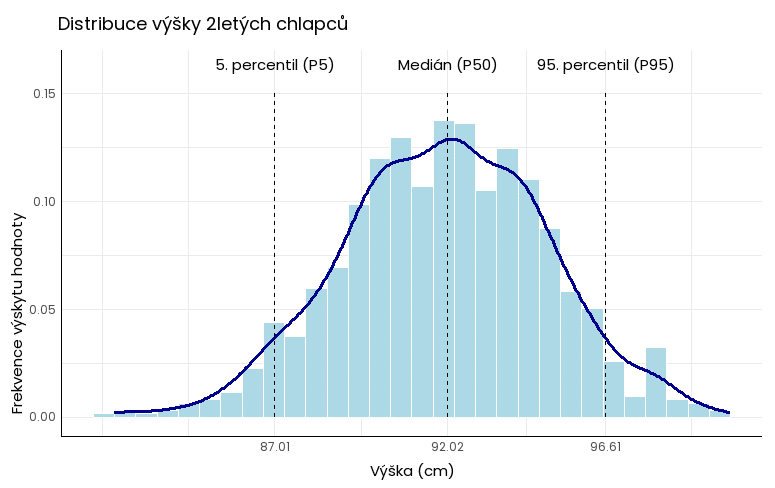
Příklad využití percentilů ve zdravotnictví: pokud je výška 2letého chlapce pod 5. percentilem (je nižší než 87 cm) či nad 95. percentilem (je vyšší než 96,6 cm), může jít o známku zdravotních problémů (např. nedostatek či nadbytek růstového hormonu). Lékař pak pacienta doporučí na další vyšetření.

Excel: funkce pro výpočet percentilu

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet percentilů
=PERCENTILE.INC(A1:A100, 0.05)  # pro výpočet P5
=PERCENTILE.INC(A1:A100, 0.2)  # pro výpočet P20
=PERCENTILE.INC(A1:A100, 0.5)  # pro výpočet P50
=PERCENTILE.INC(A1:A100, 0.95)  # pro výpočet P95

R: kód pro výpočet percentilu

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet percentilů P5, P20, P50 a P95
quantile(data, probs = c(0.05, 0.2, 0.5, 0.95))

Hromadný výpočet souboru popisných charakteristik v jazyce R

Pro získání základního přehledu o vlastnostech datového souboru slouží příkaz summary(), rozsáhlejší přehled získáte příkazem describe().

Příkazem summary() vypočítáte:

• minimální a maximální hodnotu datového souboru,
• hodnotu 1. a 3. kvartilu a mediánu (tedy 25., 50. a 75. percentil),
• aritmetický průměr,
• počet pozorování pro jednotlivé kategorie/úrovně (u nominálních a ordinálních proměnných).

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# výpočet souboru popisných charakteristik s funkcí summary
summary(data)

Příkazem describe() (je součástí balíčku psych, který je třeba nainstalovat a načíst) spočítáte:

• počet platných a chybějících pozorování,
• minimální a maximální hodnotu datového souboru a jeho rozsah,
• medián (50. percentil) a medián absolutních odchylek,
• aritmetický průměr a a oříznutý průměr (průměr po odstranění určitého procenta nejnižších a nejvyšších hodnot),
• směrodatnou odchylku a směrodatnou chybu průměru,
• špičatost datového souboru (rozložení hodnot v porovnání s normální distribucí),
• šikmost datového souboru.

# načtení knihovny
library(psych)

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# výpočet souboru popisných charakteristik s funkcí describe
describe(data)