V minulém článku o základních statistických pojmech jsme mj. blíže vysvětlili, co je statistický soubor, jednotka a znak a jak tyto pojmy zapadají do celkové analýzy dat.
V tomto článku se budeme věnovat poslednímu zmíněnému pojmu, statistickým znakům (proměnným) – tedy vlastnostem objektu či jevu, který zkoumáme (např. výška žen) a jež mohou nabývat různých hodnot (např. 156 cm, 162 cm a 179 cm).
Než ale s výzkumem vůbec začneme, musíme mj. určit:
- jaké proměnné je třeba měřit, abychom vůbec měli šanci zjistit odpovědi na pokládané výzkumné otázky (a tedy vyvrátit či nevyvrátit nulovou – tedy zkoumanou – hypotézu),
- zda je měření těchto proměnných technicky, finančně a eticky proveditelné,
- mezi jaký typ měřené proměnné patří, abychom mohli zvolit vhodné statistické metody a získat výsledky s vypovídající hodnotou (viz dále).
Příklad – studie vlivu kofeinu na srdeční tepPokud např. zkoumáme vliv kofeinu na frekvenci srdečního tepu u zdravých dobrovolníků, budou nás zajímat tyto proměnné:
Relevantní proměnnou by mohla být např. také hladina adrenalinu v krvi v různých časových úsecích před podáním kofeinu a po něm. Toto měření je ale technicky náročnější, neboť vyžaduje odběr a rozbor krve. 
Zvýhodněné balíčky kurzů
Zakupte si balíček 2 nebo více vybraných kurzů a ušetřete Mohli bychom také měřit míru vazby kofeinu na adenosinové receptory v mozku, studium této proměnné je ale zase neprůchozí eticky (je k němu totiž potřeba mj. odebrat mozkovou tkáň). Naopak nemá smysl zabývat se proměnnými jako příjem, výška či barva kůže jednotlivých účastníků studie. Tyto znaky totiž pravděpodobně neovlivňují působení kofeinu na srdeční tep. |
Všechny proměnné můžeme rozdělit podle:
- hodnot, jakých při měření měření nabývají (a vzájemného poměru techto hodnot),
- vzájemné závislosti.
Terminologie různých druhů statistických znaků je často matoucí – řada typů proměnných má někdy i 4 různé druhy označení. Základní rozdělení shrnuje tato infografika (kliknutím zvětšete):
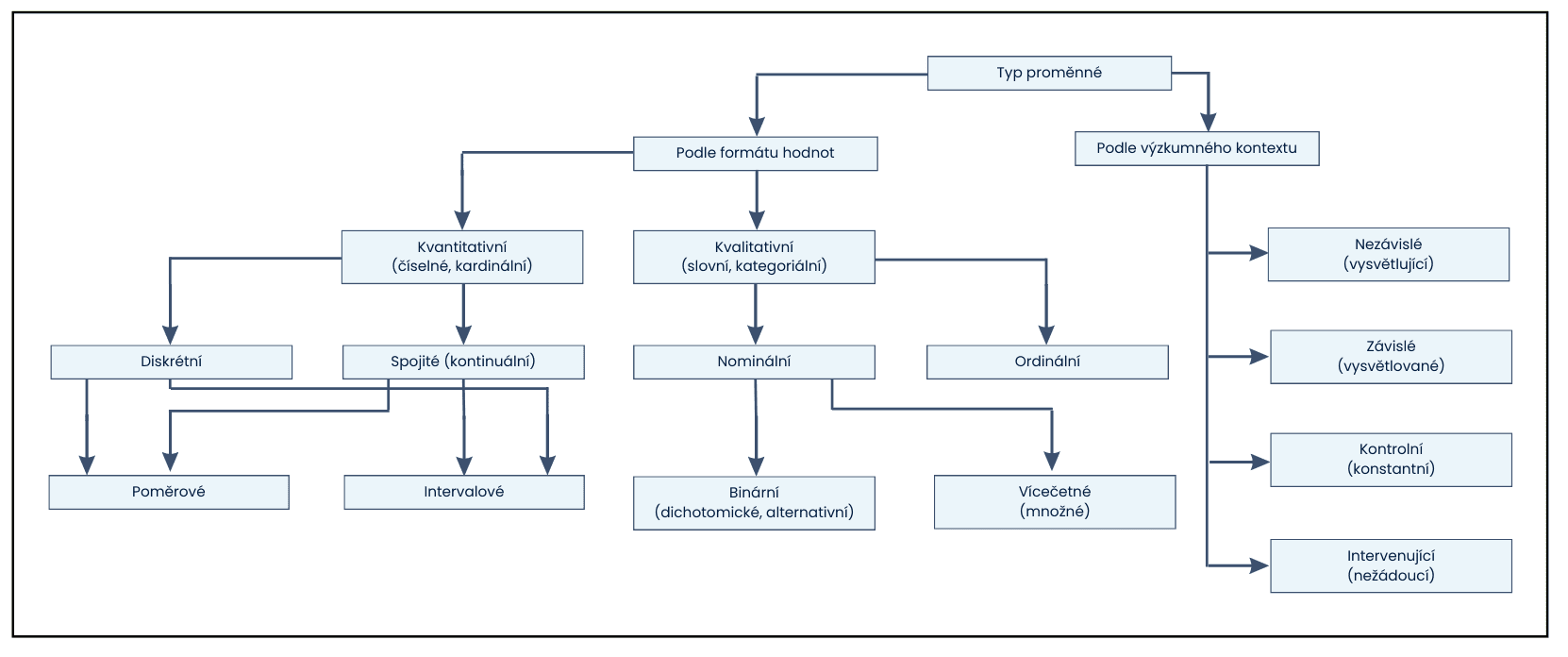
Většina proměnných spadá do více tříd. Například výška člověka je kvantitativní, poměrový a závislý znak (pokud jej zkoumáme v souvislosti s jinými faktory).
Kvantitativní proměnné
Kvantitativní proměnné (v české literatuře také jako číselné, metrické či kardinální) jsou takové, které nabývají číselných hodnot.
Je s nimi možné zpravidla provádět běžné matematické operace a lze je vyhodnocovat pomocí všech metod popisné statistiky. Kvantitativní statistické znaky dělíme na diskrétní a spojité:
Diskrétní proměnné
Nabývají pouze určitých, zpravidla celočíselných hodnot.
Možné matematické operace: sčítání, odčítání, dělení a násobení
Možné operace popisné statistiky: průměr, medián, modus, rozptyl ad.
Příklady diskrétních proměnných: množství účastníků studie, počet planet ve Sluneční soustavě, počet listů na rostlině
Spojité (kontinuální) proměnné
Tereoticky nabývají nekonečného množství hodnot.
Možné matematické a statistické operace: viz níže
Příklady spojitých proměnných: váha účastníků studie, průměr planet Sluneční soustavy nebo spotřeba kyslíku rostlinou
V praxi jsou hodnoty spojitých znaků často limitované určitým intervalem. Např. je nereálné, aby člověk vážil 10 000 kg nebo aby průměr planety dosáhl 10násobku průměru Slunce (došlo by k jejímu gravitačnímu zhroucení do hvězdy).
|
Pokud bychom zašli do detailu, jsou všechny spojité znaky ve skutečnosti diskrétní. Např. spotřeba kyslíku určitou rostlinou činí celočíselný počet molekul kyslíku, průměr planety je zase celočíselným násobkem Planckových délek (nejmenší možné vzdálenosti). Z praktického hlediska ale tyto proměnné bereme jako spojité. |
Diskrétní i spojité proměnné můžeme dále rozdělit podle vzájemného vztahu měřených hodnot na intervalové a poměrové:
Intervalové kvantitativní proměnné
Mají rovnoměrné rozdíly mezi hodnotami, ale nemají nulovou hodnotu ve smyslu neexistence dané vlastnosti.
Možné matematické operace: sčítání a odčítání
Možné operace popisné statistiky: průměr, medián, modus, rozptyl ad.
Příklady intervalových proměnných: teplota ve stupních Celsia, pH roztoku, kalendářní rok
U intervalových znaků nelze změřit poměr mezi různými hodnotami. Např.:
- 0 °C neznačí neexistenci teploty, ale pouze z dalších možných hodnot; proto neplatí, že by 40 °C bylo dvakrát vyšší než teplotou než 20 °C,
- hodnota 0 u pH neznamená absenci kyselosti, ale extrémně silnou kyselinu,
- rok 0 neznačí absenci kalendáře či času, ale pouze přelom letopočtu.
Poměrové kvantitativní proměnné
Mají rovnoměrné rozdíly mezi hodnotami. Nulová hodnota značí, že daná proměnná u studovaného objektu či jevu neexistuje.
Přípustné matematické operace: sčítání a odčítání, dělení a násobení (s výjimkou nulové hodnoty)
Přípustné metody popisné statistiky: průměr, medián, modus, rozptyl ad.
Příklady poměrových proměnných: teplota ve stupních Kelvina (viz níže), koncentrace soli v roztoku, cena zboží
U intervalových znaků lze změřit poměr mezi různými hodnotami. To znamená, že:
- 0 K (absolutní nula) skutečně značí absenci teploty (při matematických operacích ji proto nelze využít); lze tak říci, že materiál o teplotě 100 K je 20krát teplejší než materiál o teplotě 5 K,
- nulová koncentrace soli (0 g/l) znamená její absenci, a proto je např. možné tvrdit, že roztok s koncentrací 8 g/l je 4krát méně koncentrovaný, než ten s 32 g/l,
- cena 0 Kč značí neexistenci ceny.
Kvalitativní proměnné
Kvalitativní proměnné (v české literatuře též jako slovní a kategoriální) nabývají hodnot v podobě slov a číselných kódů. Pro kvalitativní hodnoty se používá také výraz obměny.
Za určitých podmínek – viz níže – je lze převést do číselného formátu a charakterizovat je popisnou statistikou. Kvalitativní znaky rozdělujeme na nominální a ordinální:
Nominální proměnné
Mezi hodnotami nominálních proměnných neexistuje žádné pořadí ani hierarchie. Podle počtu možných obměn dělíme nominální znaky na:
- binární (dichotomické, alternativní) proměnné – nabývají přesně dvou možných hodnot,
- vícečetné (množné) proměnné – nabývají tří a více možných hodnot.
Možné matematické operace: žádné
Možné operace popisné statistiky: modus, četnost
Pozor, s nominálními hodnotami ve formě číselných znaků (např. čísla tramvajových linek) nelze provádět běžné matematické operace ani je vyhodnocovat metodami popisné statistiky.
Příklady binárních nominálních proměnných: výsledek těhotenského testu, souhlas s tvrzením v dotazníku, přítomnost určitého prvku ve vzorku
Binární proměnné se často kódují čísly 0 a 1 (např. nepřítomnost prvku ve vzorku = 0, přítomnost prvku ve vzorku = 1).
Příklady vícečetných nominálních proměnných: skupiny minerálů (silikáty, karbonáty, sulfáty, halogenidy, oxidy), typy krevních skupin (A, B, AB, O), druhy chemických reakcí
Ordinální proměnné
U hodnot ordinálních proměnných vždy existuje určité uspořádání nebo hierarchie. Jednotlivé obměny je možné seřadit, není ale možné určit velikost rozdílů mezi nimi.
Možné matematické operace: žádné
Možné operace popisné statistiky: medián, modus, četnost
Příklady ordinálních proměnných: školní známkování, stádia nádorového onemocnění, Mohsova stupnice tvrdosti minerálů.
Příklad – studie vlivu kofeinu na srdeční tepVe výzkumu vlivu kofeinu na frekvenci srdečního tepu u zdravých dobrovolníků bychom výše zmíněné statistické znaky (diskrétní, spojité, nominální, ordinální) roztřídili takto:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proměnné podle závislosti a vlivu na výzkum
Podstatou naprosté většiny experimentů je změna určitých podmínek a sledování jejich dopadu na jev či objekt, který zkoumáme. Z tohoto pohledu tak můžeme statistické znaky rozdělit – kromě výše zmíněného dělení – na závislé, nezávislé, kontrolní a rušivé.
Nezávislé (vysvětlující) proměnné jsou takové, nad kterými máme kontrolu, během experimentu cíleně měníme jejich hodnoty a u nichž předpokládáme, že ovlivňují hodnoty závislých proměnných. V grafech se standardně vynáší na osu x.
Závislé (vysvětlované) proměnné jsou pak ty, jejichž hodnoty měříme a vyhodnocujeme pomocí statistických testů. V grafech se typicky vynáší na osu y.
Jako kontrolní (konstantní) označujeme proměnné, které během experimentu nijak nemění své hodnoty.Rozlišujeme také intervenující (nežádoucí) proměnné, které mohou do naší studie vnášet chybu a zkreslují její výsledky. Proto se je pokud možno snažíme odstranit.
Příklad – studie vlivu kofeinu na srdeční tepJak bychom rozdělili vztah jednotlivých statistických znaků v naší kofeinové studii?
Intervenující proměnnou v této studii by byla např. přítomnost onemocnění, které mění srdeční tep (třeba tachykardie či bradykardie). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Aby to nebylo tak jednoduché, termíny závislého a nezávislého znaku můžeme použít pouze u experimentálního výzkumu, který se zabývá vlivem skupiny proměnných na jiný soubor proměnných. U korelačního výzkumu, který zkoumá vztah mezi jednotlivými proměnnými (nikoliv závislost), používáme neutrální označení proměnná A a proměnná B, někdy také přecházející a následující proměnná (tato terminologie ale může naznačovat kauzalitu). |
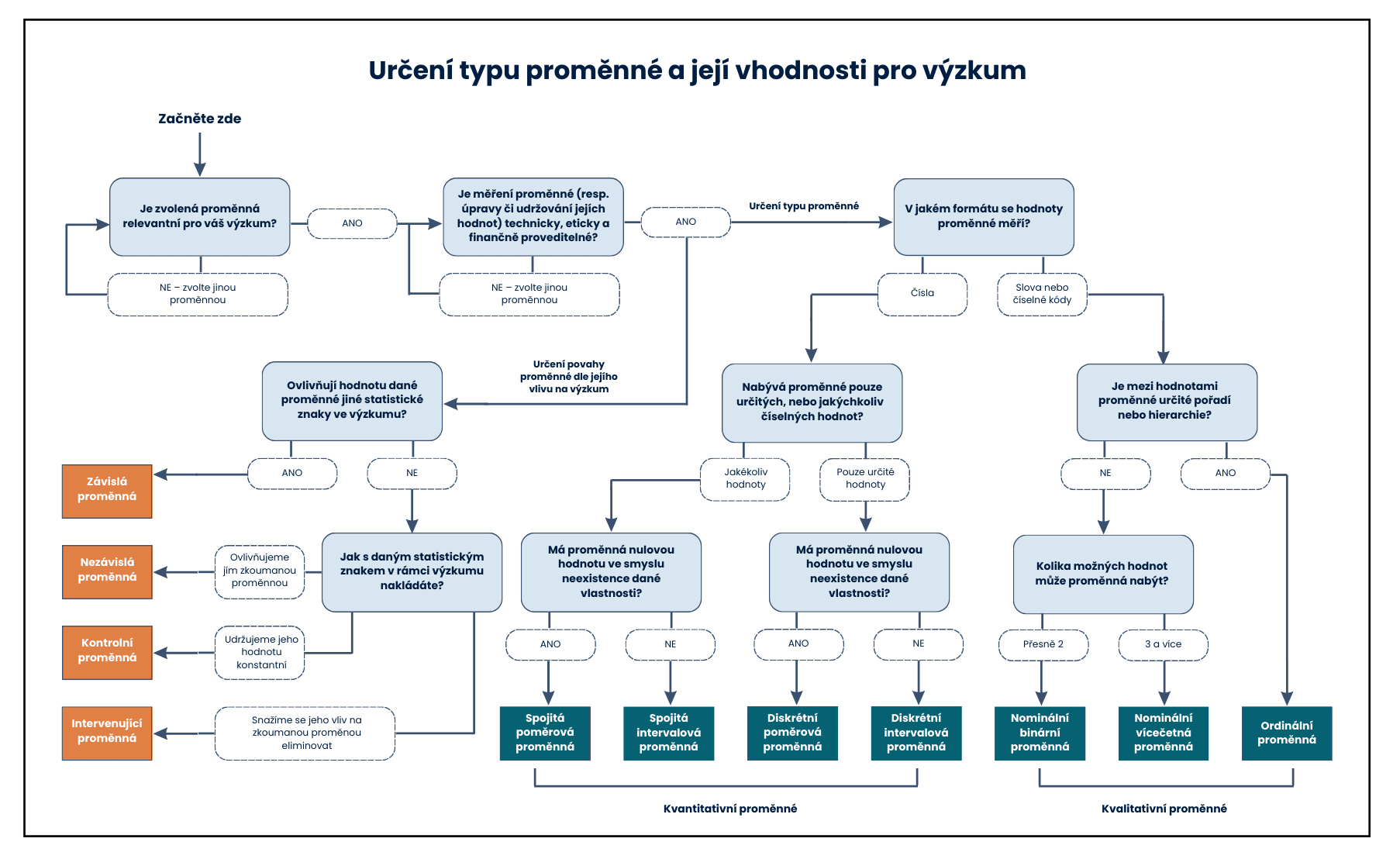
Diagram: Jak určit typ proměnné (a zda je vhodná pro váš výzkum)
Pro snazší určení druhu statistických znaků jsme pro vás vytvořili diagram níže. Pomůže vám také vyhodnotit, zda je měření dané proměnné vůbec proveditelné (diagram zvětšíte kliknutím):
 Poslední místa –
Poslední místa –