Pro správný vhled do statistických metod se hodí znát základní terminologii oboru – jakkoliv intuitivně mohou jednotlivé výrazy znít. Orientaci vám usnadní rozcestník na levém okraji.
Statistika
Statistika samotná je vědecký obor, který se zabývá sběrem, zpracováním, prezentací a interpretací dat o nějakém jevu nebo skupině objektů. Využívá k tomu řadu matematických metod a principů, které nám umožňují o daném jevu, resp. skupině objektů, vyvozovat – s určitou mírou jistoty – závěry a předpovědi.
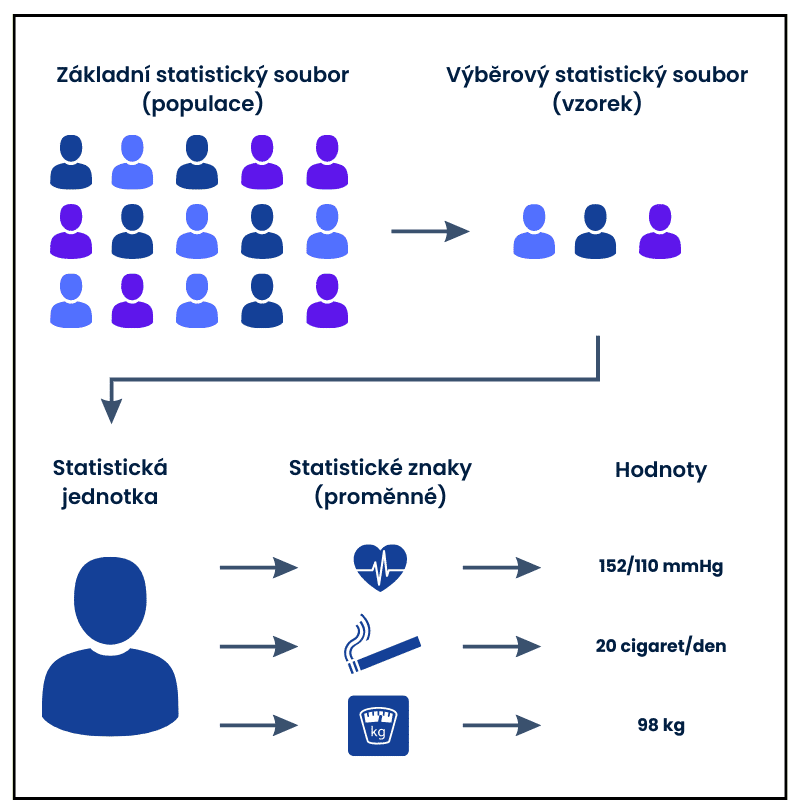
Statistická jednotka
Statistická jednotka je základní prvek, který zkoumáme. Je možné jej vymezit věcně (studujeme určitý objekt či jev) a popř. také prostorově (studujeme jednotky v určité oblasti) a časově (studujeme jednotky v určitém období jejich existence).
Příklady statistických jednotek
|
Statistický soubor
Základní statistický soubor (populace) je skupina všech statistických jednotek, které existují.
Příklady základních statistických souborů (populací)
|
Pokud není možné studovat základní statistický soubor vcelku, přistupujeme k výběrovému statistickému souboru (vzorkům), tedy jen k určité části statistických jednotek. Vzorky vybíráme tak, aby reprezentovaly vlastnosti dané populace. Jen tak můžeme informace zjištěné zkoumáním výběrového statistického souboru vztáhnout na celý základní statistický soubor.

Zakupte si balíček 2 nebo více vybraných kurzů a ušetřete
Příklady výběrových statistických souborů (populací)
|
Důležitým termínem je rozsah souboru, značící celkový počet statistických jednotek ve studovaném statistickém souboru (např. již zmíněných 500 hypertoniků). Standardně se označuje písmenem N.
Statistický znak (proměnná)
Statistický znak (také proměnná) je vlastností statistické jednotky, kterou můžeme změřit např. na přístroji nebo dotazníkovým šetřením.
Standardní označení: x
Příklady statistických znaků (proměnných)
|
Statistické znaky se dělí na kvantitativní a kvalitativní a dále do dalších kategorií – přečtěte si o různých typech proměnných.
Hodnoty (data)
Hodnotami vyjadřujeme stav konkrétního pozorování či měření sledovaných proměnných.Standardní označení: xi (x1 pro hodnotu proměnné u 1. jednotky, x2 pro pro hodnotu proměnné u 2. jednotky ad.)
Příklady hodnot sledovaných proměnných
|
Synonymem pro skupinu proměnných a jejich hodnot jsou označení soubor dat a datová sada – tedy termíny, se kterými při analýze dat běžně pracujeme.
Četnost
Četností rozumíme počet opakování určité hodnoty zkoumaného statistického znaku (proměnné) v daném statistickém souboru. Dělíme ji na:
- absolutní četnost – udává celkový počet opakování dané hodnoty (standardní označení absolutní četnosti: ni – n1 pro určitou hodnotu, n2 pro jinou hodnotu atd.),
- relativní četnost – udává podíl opakování dané hodnoty k celkovému rozsahu souboru, tedy ni/N (standardní označení relativní četnosti: fi – f1 pro určitou hodnotu, f2 pro jinou hodnotu atd.),
- kumulativní četnost – udává (absolutní i relativní) počet či podíl opakování do určité hodnoty.
Příklady hodnot sledovaných proměnnýchPředstavte si, že ve studovaném souboru 500 jedinců s vysokým krevním tlakem udává 125 hypertoniků, že si denně dopřejí přesně 10 cigaret. Četnost těchto jedinců pro sledovanou proměnnou (počet vykouřených cigaret) v daném souboru je potom:
Pokud je v souboru navíc 100 jedinců (n2), kteří vykouří denně 5 cigaret, a 100 nekuřáků (n3), můžeme spočítat kumulativní četnost hypertoniků, kteří nekouří, nebo kouří do 10 cigaret denně. (Předpokládáme, že zbytek jedinců v souboru kouří více než 10 cigaret denně – ti nás ale teď nezajímají.)
|
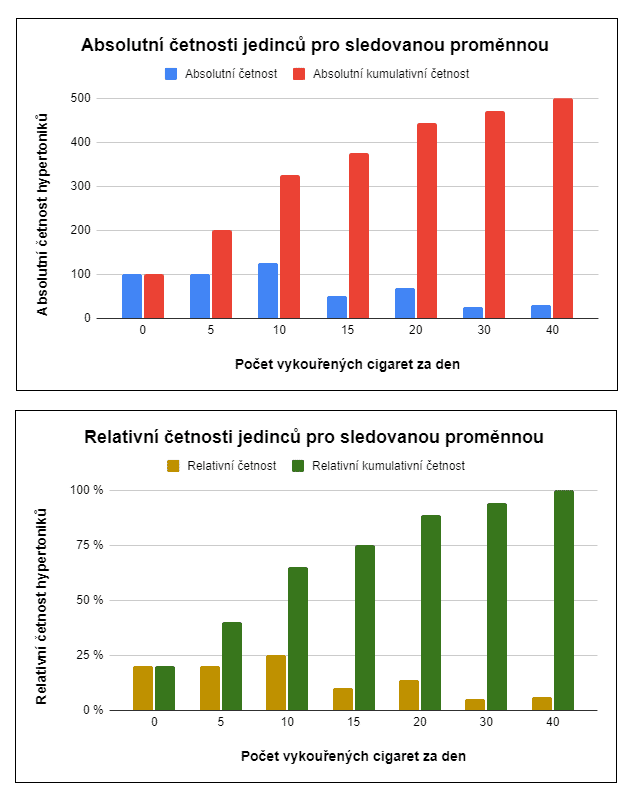
Absolutní a kumulativní četnosti není kvůli rozdílnému měřítku vhodné zobrazovat ve stejném grafu. Zde jsme udělali výjimku – detailní informace najdete v připravovaném článku.
Četnost můžete vypočítat jak u diskrétních proměnných (mohou nabývat jen určitých hodnot, např. počet cigaret za den), tak – za určitých podmínek – u spojitých proměnných (nabývají jakýchkoliv hodnot, např. tělesná hmotnost). Na toto téma pro vás připravujeme samostatný článek.
Další pojmy ze statistiky
Do statistické analýzy patří samozřejmě řada dalších termínů. Jejich detailnější popis naleznete po kliknutí na danou frázi.
Rozdělení dat (hodnot) – udává, s jakou pravděpodobností nabyde sledovaná proměnná určitých hodnot. Ve statistické analýze pracujeme nejčastěji s normálním (Gaussovým), rovnoměrným binomickým či Poissonovým rozdělením.
Hypotéza – předpoklad o určité statistickém souboru (populaci) a sledovaných proměnných, který se snažíme s pomocí vzorků a statistických testů vyvrátit, resp. nevyvrátit. Ve výzkumu standardně pracujeme s:
- nulovou hypotézou H0 (mezi sledovanými proměnnými neexistuje žádný vztah – pokud např. u vzorku pozorujeme snížení tlaku po podání léku, jedná se o jev vzniklý náhodou),
- alternativní hypotézou H1 (mezi sledovanými proměnnými existuje určitý vztah a pozorovaný jev – např. snížení tlaku po podání léku – nevzniká náhodou).
Popisná (deskriptivní) statistika – pomocí průměru, mediánu, rozptylu, směrodatné odchylky, koeficientu špičatosti a dalších metrik popisuje vlastnosti proměnných, který analyzujeme. Popisná statistika pomáhá také, určit, kterou metodu induktivní statistiky využít pro zamínutí nulové hypotézy (viz výše).
Induktivní (inferenční) statistika – pomáhá určit, zda je platná nulová, nebo alternativní hypotéza, a zda vztah sledovaných proměnných ve vzorku (experimentální lék snižuje tlak u 500 hypertoniků) platí pro celou populaci (experimentální lék snižuje tlak u všech hypertoniků). Mezi základní metody induktivní statistiky patří:
- t-test (Studentův test),
- analýza rozptylu (ANOVA),
- korelační analýza,
- regresiní analýza.
 Poslední místa –
Poslední místa –