Analýza dat ve vědě a výzkumu

Pozor, tento článek je dlouhý. U tak obsáhlého oboru, jakým statistika je, to jinak ani nejde. Přesto do jednotlivých metod příliš nezabíháme – cílem textu je ujasnit, na jakých principech analýza dat ve výzkumu stojí a proč byste jí měli věnovat svůj čas.

Sběr, úprava a vyhodnocování experimentálních dat jsou nedílnou součástí každého výzkumu. Nutno dodat, že ne zrovna oblíbenou. Statistika může na první pohled vypadat složitě – a navíc jen málokdy se vyučuje tak, aby podstatu jednotlivých metod pochopil opravdu každý.

Výsledkem je situace, kdy podstatná část vědců roky vyhodnocuje experimenty základními statistickými testy – a z obavy, že udělají chybu, se vyhýbají pokročilejším metodám. Ty vám přitom mohou pomoct např. potvrdit složitější hypotézy, vytvořit komplexní modely chování většího množství proměnných nebo najít skryté vztahy mezi různými soubory dat.

Jednoduše řečeno: pokročilá statistika je klíčem ke kvalitnějším výsledkům, otevře vám dveře do prestižních vědeckých publikací a – v kombinaci s moderní správou dat – zvýší vaše šance na získání grantu.

Ale nepředbíhejme a nejprve se podívejme na:

• možnosti, jak experiment s ohledem na jeho vyhodnocení navrhnout,
• základní statistické pojmy a metody,
• jednotlivé kroky procesu datové analýzy.

Pojmem „statistika“ myslíme kvantitativní datovou analýzu, která se zabývá vyhodnocováním číselných a kategoriálních proměnných. Cílem statistiky je 1) určit velikost rozdílu mezi dvěma a více skupinami, 2) určit povahu vztahu mezi proměnnými, 3) otestovat platnost určité hypotézy. Tím se liší od kvalitativní analýzy, která zkoumané fenomény (např. vnímání dopadů depresivní poruchy na život z pohledu pacienta) hodnotí převážně slovně. Více informací najdete v článku typy proměnných.

Analýza vědeckých dat v praxi

Pod datovou analýzou si řada lidí představí složitou terminologii, vzorce a teoretické poučky o rozložení pravděpodobnosti. O ničem z toho dnes mluvit nebudeme. Naopak se podíváme, jak a proč nás data bádáním provázejí.

Představte si, že máte v rukou – či ve zkumavce – lék, který podle předběžných výsledků snižuje vysoký krevní tlak. Z jakých kroků byste měli sestavit výzkum, který účinek preparátu potvrdí nebo vyvrátí?

1. formulování výzkumného problému, výzkumné otázky a hypotézy (nový lék pomáhá s určitou jistotou snížit hypertenzi lépe než placebo),
2. určení typu proměnných, které se budou měřit (v tomto případě hodnoty systolického tlaku – pro různé druhy proměnných jsou vhodné různé statistické metody),
3. výběr reprezentativního vzorku dobrovolníků s vysokým krevním tlakem do klinické studie,
4. vlastní experiment, tedy např. podávání preparátu s účinnou látkou deseti dobrovolníkům (experimentální skupina) a podávání placeba jiné desítce dobrovolníků (kontrolní skupina),
5. sběr experimentálních dat měřením krevního tlaku před a po podání obou přípravků,
6. kontrola datové kvality, tedy např. určení toho, zda jsou data konzistentní a neobsahují extrémní hodnoty (třeba následkem vadného tlakoměru),
7. čištění dat (mj. odstranění duplicitních a odlehlých hodnot – část těchto kroků se provádí po vypočtení základních charakteristik datového souboru metodami popisné statistiky, viz bod 9),
8. datová transformace, např. pokud se data z tlakoměru ukládají ve formátu nevhodném pro další zpracování,
9. využití popisné statistiky pro výpočet základních parametrů získaných dat (např. určení mediánu, rozptylu a směrodatné odchylky hodnot krevního tlaku před a po podání léku, resp. placeba),
10. vizualizace základních statistických parametrů (např. krabicový graf pro srovnání mediánu krevního tlaku mezi jednotlivými skupinami) a určení typu rozložení dat (viz níže),
11. výpočet p-hodnoty (viz dále) pomocí vhodné statistické metody a vyvrácení či nevyvrácení hypotézy (např. využití párového t-testu pro zjištění, zda nový lék snižuje krevní tlak významněji než placebo).

Připadáte si zahlcení? Žádný strach – na následujících řádcích si vysvětlíme, co zmíněné pojmy přesně znamenají a k čemu je ve svém výzkumu využijete.

Formulování hypotézy

Hypotézy jsou základem každé výzkumné otázky. Vycházejí z dobře formulované výzkumné otázky a vždy proti sobě stojí nejméně dvě:

• Nulová hypotéza (H₀) říká, že mezi srovnávanými daty neexistuje žádný významný rozdíl, např. že zkoumaný lék na hypertenzi má stejný účinek jako placebo.
• Alternativní hypotéza (H₁) pak tvrdí, že mezi porovnávanými daty je významný rozdíl, tedy: zkoumaný lék na vysoký krevní tlak má jiný účinek než placebo (samozřejmě doufáme, že hypertenzi snižuje). Alternativní tvrzení je vlastně důvodem, proč celý výzkum provádíme.

Žádnou nulovou hypotézu nelze absolutně přijmout či zamítnout, protože vždy pracujeme s určitou pravděpodobností. Ve výzkumné praxi se jako hladina spolehlivosti obvykle přijímá 95 %, která vyjadřuje, s jakou pravděpodobností by se výsledky studie opakovaly, pokud bychom ji znovu provedli.

Zbylých 5 % je potom hodnota hladiny významnosti (ɑ). Ta zase sděluje pravděpodobnost, že pozorovaný rozdíl mezi nulovou a alternativní hypotézou vznikl náhodou (a není tedy výsledkem toho, že by zkoumaný lék byl skutečně účinnější než placebo).

Při určení toho, která hypotéza je pravděpodobně platnější, počítáme tzv p-hodnotu (signifikanci – viz dále). Pokud je p-hodnota:

• nižší než hladina významnosti (tedy nižší než 0,05), potom zamítáme nulovou hypotézu a přijímáme alternativní hypotézu („zkoumaný lék snižuje hypertenzi účinněji než placebo“),
• vyšší než hladina významnosti (tedy vyšší než 0,05), potom zamítáme alternativní hypotézu a přijímáme nulovou hypotézu („zkoumaný lék má na hypertenzi stejný účinek jako placebo“).

S testováním hypotéz se pojí i tzv. chyby I. a II. typu – ty probereme v samostatném článku.

Určení typu dat (proměnných)

Pro správnou analýzu experimentálních dat je důležité vědět, jaké typy proměnných existují a jak vypadají (podle toho mj. volíme vhodné statistické testy). Jednotlivé kategorie dat shrnuje tato infografika:

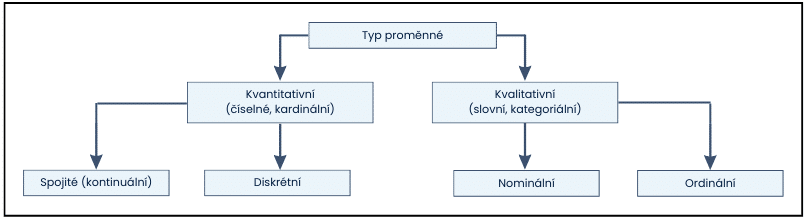
Kvalitativní proměnné jsou takové, které nelze jednoduše vyjádřit číselně. Formulují se pomocí popisů, kategorií či vlastností a dělíme je na:

• Nominální proměnné – lze zařadit do kategorií, není mezi nimi ale žádné pořadí či hierarchie. Příkladem jsou skupiny minerálů (silikáty, karbonáty, sulfáty, halogenidy, oxidy), typy krevních skupin (A, B, AB, O) či druhy chemických reakcí.
• Ordinální proměnné – tyto proměnné lze také řadit do kategorií, navíc mezi nimi existuje určité pořadí či hierarchie – např. stádia nádorového onemocnění (I až IV), hierarchie genové exprese (transkripce, pre-mRNA úpravy, translace, posttranslační úpravy) či Mohsova stupnice tvrdosti minerálů.

Kvantitativní proměnné (se kterými budete ve svém výzkumu pravděpodobně pracovat nejčastěji) se vyjadřují číselnými hodnotami a je možné je vyhodnotit statistickými a matematickými metodami.

• Diskrétní proměnné – tyto proměnné mohou nabývat pouze celočíselných hodnot, např. množství účastníků klinické studie, počet kopií zkoumaného genů v buňce či počet případů nového onemocnění za rok.
• Spojité (kontinuální) proměnné – nabývají jakýchkoliv číselných hodnot. Příkladem je objem roztoku ve zkumavce, tělesná teplota pacienta nebo hmotnost vzorku horniny.

Příklad – zkoumání léku na hypertenzi S jakými typy proměnných bychom pracovali u testování nového léku proti vysokému tlaku? Při pohledu na typický tlakoměr bychom hádali, že systolický tlak nabývá pouze celočíselných hodnot (diskrétní data). Ve skutečnosti jde ale pouze o formát daného přístroje, který naměřená čísla zaokrouhluje. Systolický tlak nabývá jakékoliv hodnoty (v rozmezí cca 0 až 370 mmHg), jde tedy o spojitý typ proměnných. Stejným druhem dat je také dávka podaného léku či placeba. Diskrétním typem proměnných je naopak počet dobrovolníků v klinické studii. Vedlejší účinky léku by pak reprezentovaly nominální proměnné (neexistuje mezi nimi žádná hierarchie), závažnost těchto účinků by byla ordinálním typem proměnných (mezi lehkou, střední a těžkou nežádoucí reakcí je jasná posloupnost).

Výběr vzorku (výzkumného souboru)

Při ověřování vědeckých hypotéz je prakticky nemožné, abychom otestovali celou zkoumanou populaci. Ve statistice rozumíme populací soubor všech jedinců, objektů či událostí, kteří mají určité vlastnosti společné a o kterých snažíme zjistit určité informace.

Příkladem populace je třeba soubor všech lidí s vysokým krevním tlakem, všech buněk s kopií zkoumaného genu, všech hornin v určitém pohoří či všech hvězd typu G ve vesmíru.

Ve výzkumné praxi proto pracujeme se vzorky z dané populace. Aby tuto populaci reprezentovaly co nejlépe, je potřeba:

1. jasně definovat zkoumanou populaci,
2. určit velikost vzorku, který danou populaci dostatečně přesně vystihuje,
3. zvolit vhodnou metodu vzorkování (náhodné, systematické nebo stratifikované; na toto téma pro vás připravujeme článek),
4. nasbírat vzorky z populace a ověřit, že danou populaci skutečně reprezentují.

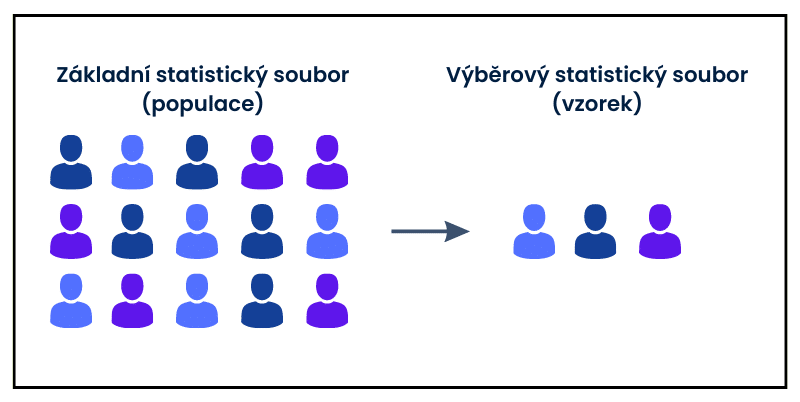
Příklad – zkoumání léku na hypertenzi Do zkoumané populace hypertoniků bychom mohli zařadit např. všechny osoby se systolickým tlakem nad 140 mmHg a s určitými souvisejícími nemocemi (diabetes II. typu a kardiovaskulární onemocnění), kteří se na hypertenzi nikdy neléčili. Kritéria je možné měnit podle potřeby.

Popisná statistika

Popisná (deskriptivní) statistika se zaměřuje na srozumitelné shrnutí a popis hlavních charakteristik datové sady (vzorku). Využívá k tomu tzv. míry četnosti, polohy, variability a tvaru. Dalším nástrojem pro popis (resp. vizualizaci) naměřených dat je celá řada grafů. Jejím cílem není vyvozovat jakékoliv závěry o vztazích či příčinách nebo vyvracet hypotézy – to je úkolem induktivní statistiky (viz níže).

Metody popisné statistiky vám pomohou:

• určit hlavní trendy v souboru dat (např. zda menšina hodnot leží pod určitým prahem),
• porovnat mezi sebou více souborů dat,
• ověřit kvalitu dat (zda neobsahují např. duplicity) a identifikovat odlehlé hodnoty, jež zkreslují celkový obraz o vlastnostech datové sady,
• připravit data pro otestování hypotézy (očištěním sady od odlehlých hodnot a dalšími transformacemi),
• určit rozložení dat (a podle toho zvolit vhodnou statistickou analýzu a velikost potřebného vzorku – viz níže),
• shrnout výsledky studie do snadno srozumitelné prezentace.

Slepice, nebo vejce? Formálně sice popisnou statistiku využíváme až po provedení pokusu a naměření hodnot, ve skutečnosti ale její metody potřebujeme už při plánování výzkumu a výzkumné otázky. Abychom totiž určili, jak velký vzorek k měření (a nevyvrácení naší hypotézy) potřebujeme, musíme vědět: 1) zda mají data normální, binomické či jiné rozložení, 2) s jakou variabilitou zkoumané proměnné v datech pracujeme. Tyto informace zjistíme použitím metod popisné statistiky na data z předchozího podobného výzkumu, pilotního studie, teoretického modelu či simulace. I proto je důležité získaná data ukládat a sdílet podle tzv. FAIR Principles – svým kolegům tím ušetříte čas a peníze při plánování výzkumu.

Mezi základní metriky popisné statistiky patří:

• velikost vzorku (viz výše),
• míry polohy,
• míry variability (popisují vzájemnou vzdálenost – rozptyl – hodnot v datové sadě),
• míry tvaru (popisují tvar rozdělení dat ve vzorku).

Tyto základní metriky nám pomáhají určit, jestli je distribuce dat ve zkoumaném souboru parametrická, nebo neparametrická.

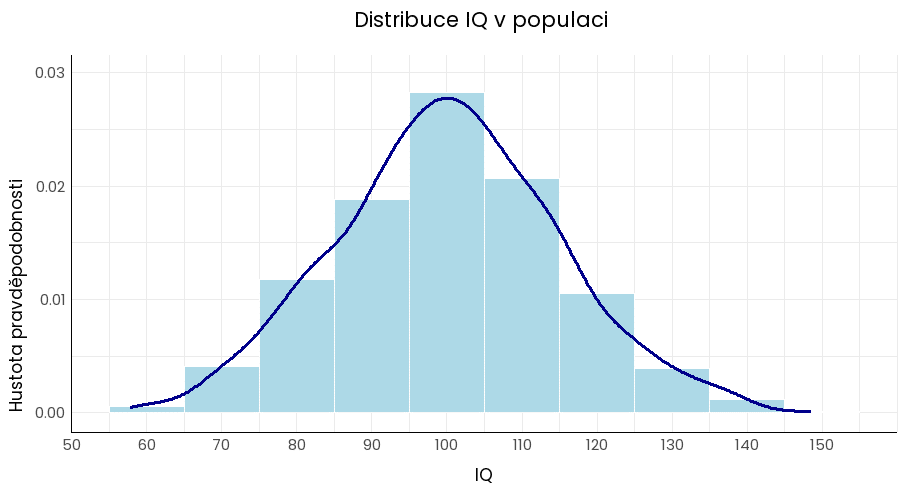
U parametrického rozdělení dat jsou jednotlivé hodnoty zkoumané proměnné ve vzorku, resp. v populaci rozdělené podle určité četnosti. Příkladem je normální rozdělení pro spojitá data (např. Gaussovo rozdělení u výšky či IQ dospělých lidí), se kterým se pracuje nejsnadněji.

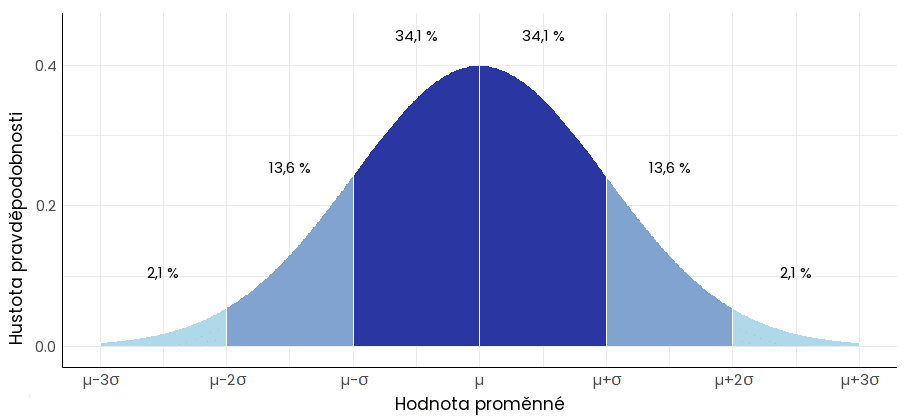
Normální rozdělení pravděpodobnosti; μ – průměrná hodnota distribuce, σ – směrodatná odchylka (udává míru rozptýlenosti hodnot kolem průměru)

Mezi další typy parametrického rozdělení dat – pro diskrétní hodnoty – patří binomické rozdělení (např. počet pacientů reagujících na léčbu), Poissonovo rozdělení (např. počet radioaktivních rozpadů za jednotku času), exponenciální rozdělení (např. doba do dalšího radioaktivního rozpadu) a rovnoměrné rozdělení (např. koncentrace léku v krvi po podání).

Při neparametrickém rozdělení dat se jednotlivé hodnoty ve vzorku, resp. v populaci neřídí určitou četností. Příkladem je srovnávání účinné dávky dvou odlišných léčebných preparátů.

K určení toho, zda je rozložení parametrické či neparametrické, slouží tzv. testy normality, které je potřeba aplikovat po vypočítání popisných statistik a před použitím induktivních metod pro ověřování hypotéz – na toto téma pro vás připravujeme samostatný článek.

Míry polohy

Tyto míry popisují různé druhy středu datového souboru. Mezi základní míry polohy patří:

• Aritmetický průměr – součet všech hodnot proměnné dělený počtem hodnot. Nevýhodou střední hodnoty je velká citlivost na odlehlé (extrémní) hodnoty, které mohou významně zkreslit celkový pohled na datový soubor.
• Medián – hodnota, která dělí hodnoty proměnné na dvě stejně velké části (poloviny). Na rozdíl od průměru není tak citlivý na extrémní hodnoty v datové sadě.
• Kvartily – rozdělují hodnoty proměnné do čtyř stejně velkých celků (čtvrtin). Podobně jako medián nejsou kvartily na odlehlé hodnoty tak citlivé jako průměr.
• Modus – zachycuje nejčastější hodnotu v datech. Nejčastěji se využívá u kvalitativních dat (např. nejčastější vedlejší účinek experimentálního léku na hypertenzi).

Pokud se hodnota aritmetického průměru a mediánu liší, znamená to, že hodnoty nejsou symetricky rozdělené – v takovém případě použijeme pro určení střední hodnoty medián.

Míry variability

Popisují různé druhy rozptylu (variability) dat okolo vypočtené střední hodnoty. Nejčastěji používané základní míry variability jsou:

• Rozpětí (variační šíře) – určuje rozdíl mezi minimální a maximální hodnotou v datové sadě. Nevypovídá nic o rozložení jednotlivých hodnot v souboru, může být navíc zkresleno extrémními hodnotami.
• Rozptyl – říká, jak moc se hodnoty proměnné rozprostírají kolem středu. Počítá se jako průměr umocněných rozdílů všech hodnot od střední hodnoty. Nevýhodou rozptylu je, že se uvádí v umocněných jednotkách a na pochopení je méně intuitivní.
• Směrodatná odchylka – vyjadřuje míru variability střední hodnoty proměnné v původních jednotkách (např. v mmHg). Čím je směrodatná odchylka vyšší, tím více jsou data rozptýlena (a jsou tedy méně konzistentní).

Míry tvaru

Vypovídají o tvaru rozdělení dat v analyzovaném souboru (a pomáhají tedy určit typ rozdělení – viz výše). Mezi základní míry tvaru řadíme:

• Koeficient šikmosti – udává asymetričnost v rozdělení dat. Pokud není koeficient šikmosti nulový (jako u Gaussovy křivky), jsou hodnoty aritmetického průměru a mediánu odlišné.
• Špičatost – měří, jak moc se data koncentrují kolem středu a tedy nakolik má křivka rozložení naměřených hodnot ostrý či plochý vrchol. Špičatost lze určit pomocí koeficientu špičatosti.

Příklad – zkoumání léku na hypertenzi Pro obě skupiny po 10 dobrovolnících jsme vypočítali tyto hodnoty popisné statistiky: Popisná statistika Tlak před podáním léku (mmHg): Tlak po podání léku (mmHg): Tlak před podáním placeba (mmHg): Tlak po podání placeba (mmHg): Průměr 157,5 137,5 150,4 148,5 Medián 157,5 137,5 150,4 148,5 Rozpětí 9 9 10 9 Rozptyl 9,17 9,17 10,27 9,17 Směrodatná odchylka 3,03 3,03 3,2 3,03 Koeficient šikmosti 0 0 -0,2 0 Špičatost -1,2 -1,2 -0,84 -1,2 Při pohledu na průměrné hodnoty se může zdát, že experimentální lék tlak skutečně snižuje. Je tomu tak ale doopravdy?

Vizualizace výsledků popisné statistiky (grafy)

Pro snazší interpretaci získaných výsledků (např. rozložení dat a určení míry polohy, viz výše) se využívají různé typy grafů. Jaké jsou ty nejčastější?

Sloupcový graf zobrazuje na ose x hodnoty proměnné, zatímco na ose y četnost těchto hodnot. Umožňuje rychle pochopit rozdíly mezi hodnotami zkoumaných kategorií a identifikovat různé trendy a anomálie. Je tedy vhodný pro nominální, ordinální a diskrétní proměnné.

Příkladem sloupcového grafu je porovnání:

• počtu případů určitého onemocnění v různých geografických oblastech,
• počtu bakterií na určitém povrchu po různé době působení dezinfekčního přípravku,
• porovnání růstových rychlostí různých druhů rostlin za stejných podmínek.

Pro zobrazení diskrétních a spojitých dat ve sloupcovém uspořádání se využívá histogram. Slouží k porovnání četnosti určité proměnné (osa y) mezi daty rozdělenými do určitých intervalů (osa x). Příkladem je třeba rozložení IQ v populaci, kdy na ose x nalezneme hodnotu inteligenčního kvocientu v určitých intervalech (např. 50–60, 60–70, 70–80 atd.) a na ose y relativní zastoupení velikosti daného IQ v populaci.

Výhodou histogramu je snadné určení střední hodnoty a vizualizace šikmosti a špičatosti v rozložení dat. Negativem tohoto grafu je jeho omezené použití pro malý datový soubor. Pro dostatečnou reprezentaci rozdělení dat je potřeba také zvolit vhodné intervaly.

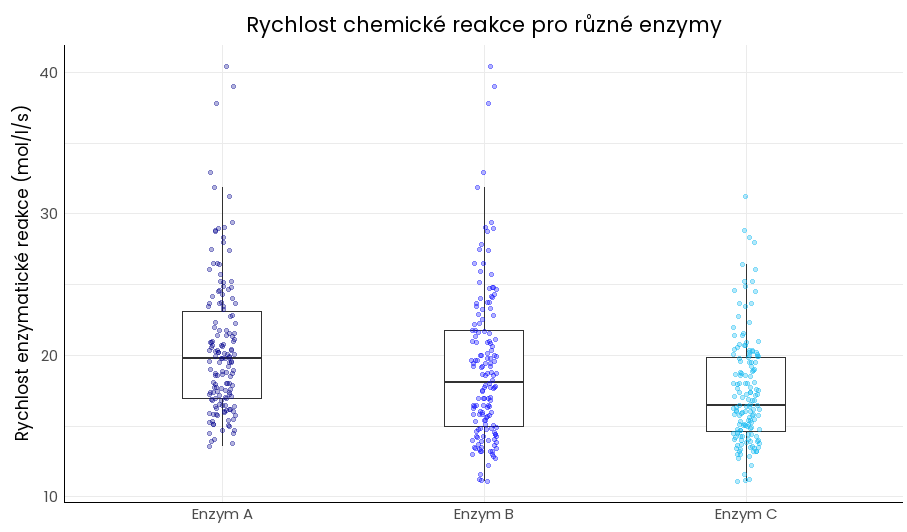
Krabicový graf (označuje se také jako box-plot) zobrazuje rozdělení dat pomocí minimální a maximální hodnoty a jednotlivých kvartilů. Samotná krabicová část zobrazuje hodnoty mezi 1. a 3. kvartilem (tzv. mezikvartilové rozpětí), nachází se v ní také hodnota mediánu. Z krabice pak vystupují tzv. vousy, které reprezentují rozsah dat mimo odlehlé hodnoty (ty jsou zobrazeny jako tečky).

Krabicový graf se – podobně jako histogram – hodí pro zobrazení intervalů ve spojitých a diskrétních datech. Příkladem použití je srovnání:

• hladiny cholesterolu v krvi osob s různými životními styly nebo stravovacími návyky,
• délky trvání určité chemické reakce při použití různých enzymů,
• účinnosti různých vakcín.

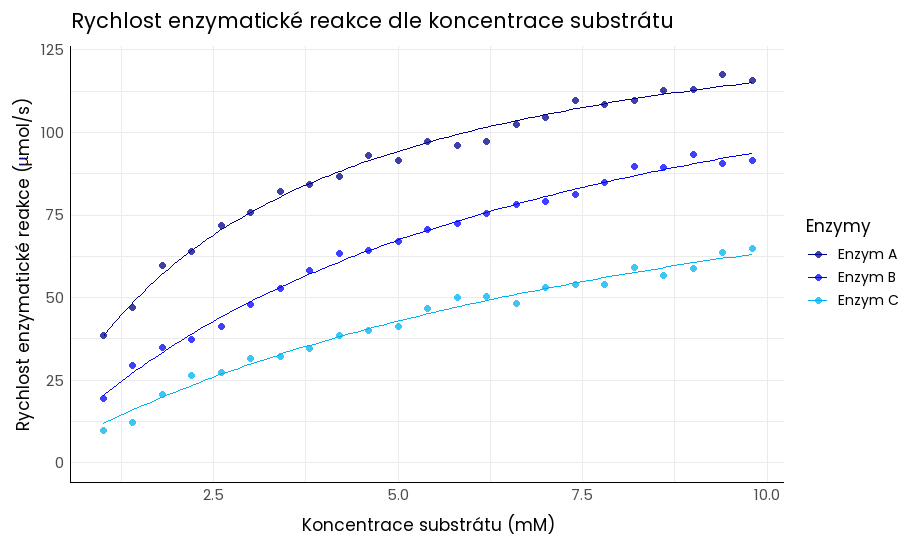
Bodový graf (scatter-plot) zobrazuje vztah mezi dvěma kvantitativními proměnnými v souřadnicovém systému. Používá se pro vizualizaci vztahu mezi dvěma spojitými nebo diskrétními proměnnými a pomůže vám identifikovat trendy, korelace, shluky nebo odchylky ve spojitých a diskrétních datech.

Hodí se např. pro zobrazení vztahu mezi:

• hladinou cholesterolu v krvi a rizikem rozvoje kardiovaskulárních onemocnění,
• koncentrací substrátu a rychlostí enzymatické reakce,
• dávkou vakcíny a její účinností.

Induktivní statistika

Účelem induktivní (inferenční) statistiky je z dat získaných zkoumáním vzorku odvodit platnost posuzované hypotézy pro celou populaci – např. zda zkoumaný lék proti hypertenzi (s určitou mírou spolehlivosti) pomůže lidem s vysokým krevním tlakem, kteří splňují stejná kritéria jako dobrovolníci v klinické studii.

Induktivní statistika se mj. snaží určit:

• rozdíly mezi dvěma a více skupinami v populaci,
• povahu a sílu vztahů mezi dvěma a více proměnnými (příklady pro jednotlivé metody najdete níže).

Vhodnou metodu vybíráme na základě výsledků popisné statistiky a typu rozdělení dat (parametrické vs. neparametrické). Ty nám také řeknou, zda nedošlo k chybě měření a zda není třeba jej opakovat.

Např. pokud u jednoho dobrovolníka naměříme tlak 20 mmHg a u druhého 400 mmHg, používáme pravděpodobně vadný tlakoměr a výsledky analýzy nám o účinnosti nového léku na hypertenzi v podstatě nic nesdělí.

Jaké základní parametrické testy pro ověření či vyvrácení hypotézy se využívají nejčastěji?

t-test

t-test (Studentův test) slouží k porovnání aritmetických průměrů jedné či dvou skupin. Využijete jej pro spojitá data s normálním rozdělením, která mají stejný, rozdílný či neznámý rozptyl. Mezi nejvyužívanější druhy t-testů patří:

• jednovýběrový t-test – porovnává průměr určité hodnoty u jedné skupiny s určitou konstantou, např. průměrný systolický krevní tlak u hypertoniků s průměrným tlakem běžné populace (ten bereme jako konstantu),
• dvouvýběrový t-test – srovnává průměr určitých hodnot u dvou nezávislých skupin, např. 1) průměrný krevní tlak u hypertoniků užívajících lék na hypertenzi a 2) průměrný krevní tlak u hypertoniků užívajících placebo,
• párový t-test – srovnává průměr určitých hodnot u dvou skupin, které na sobě závisí, např. průměrný krevní tlak u hypertoniků 1) před podáním léku, 2) po jeho podání.

ANOVA

ANOVA (analýza rozptylu) porovnává aritmetické průměry sledované proměnné (např. krevního tlaku) u více než dvou skupin (např. pacientů užívajících lék A, pacientů užívajících lék B a pacientů užívajících placebo) v závislosti na jednom či více faktorech.

Stejně jako t-test využijete ANOVA u spojitých dat s normálním rozdělením, rozptyl sledované proměnné ale musí být homogenní (na podobné úrovni).

Je také důležité, aby zkoumaná hodnota (třeba výška krevního tlaku) nebyla závislá na jiných faktorech (nedává např. smysl do klinické studie s hypertoniky zařazovat vrcholové sportovce). Podle počtu faktorů rozlišujeme:

• jednofaktorovou ANOVA – např. zkoumání závislosti průměrného krevního tlaku u tří skupin dobrovolníků v závislosti na podávaném přípravku,
• dvoufaktorovou ANOVA – např. zkoumání závislosti tlaku u tří skupin dobrovolníků na podávaném přípravku a pohlaví,
• vícefaktorovou ANOVA – např. zkoumání závislosti tlaku u tří skupin dobrovolníků na podávaném přípravku, pohlaví a věkové skupině.

Korelační analýza

Cílem korelační analýzy je zjistit, zda existuje vztah mezi dvěma kvantitavními proměnnými, tedy jestli při změně hodnoty jedné proměnné dochází ke změně hodnoty druhé proměnné. Tento test je vhodný pro kvantitativní data, která mají lineární vztah.

Korelace se vyjadřuje v hodnotách mezi -1 a 1:

• při kladné korelaci roste s hodnotou první proměnné i hodnota druhé (a naopak), např. s vyšším objemem srážek je tendence nárůstu objemu biomasy rostlin,
• při nulové korelaci se při změně hodnoty první proměnné hodnota druhé proměnné nijak nemění,
• při negativní korelaci s nárůstem hodnoty první proměnné dochází k poklesu hodnoty druhé proměnné (a naopak), např. s vyšší dávkou léku proti hypertenzi je tendence výraznějšího snížení systolického tlaku.

Pozor, korelace neznamená kauzalitu. Vždy tak např. berte v potaz, že za snížením krevního tlaku po podání léku nemusí stát účinná látka, ale jiné faktory.

Regresní analýza

Pokud zjistíme, že mezi dvěma proměnnými existuje určitý vztah (korelace), je typicky naším dalším krokem snaha popsat (typicky vzorcem), jak přesně změna hodnoty jedné proměnné ovlivní změnu hodnoty druhé. K tomu slouží regresní analýza. Podle povahy vztahu obou proměnných se rozlišuje:

• lineární regrese – popisuje lineární vztah, např. změnu krevního tlaku v závislosti na hladině cholesterolu v krvi,
• polynomiální regrese – popisuje nelineární vztah, např. změnu růstu bakterií v průběhu času,

logistická regrese – popisuje vztah nezávislé proměnné a závislé binární proměnné (nabývá jen dvou hodnot), např. zda při konzumaci energetických nápojů hrozí zvýšené riziko tvorby ledvinových kamenů (ano/ne).

Příklad – zkoumání léku na hypertenzi Po zpracování popisných statistik jsme použitím vhodného testu normality zjistili, že data mají normální rozdělení. Platnost naší hypotézy („experimentální lék účinně snižuje vysoký krevní tlak“) tedy můžeme vyhodnotit pomocí jednoho z výše zmíněných parametrických testů. Naším cílem je srovnat průměrný tlak před podáním přípravku a po jeho podání. Tyto dvě hodnoty na sobě závisí, protože účinek přípravku (placeba nebo léku) počítáme u každého jednotlivého pacienta. Pro vyhodnocení tedy zvolíme párový t-test (viz popis výše – další podmínky jeho užití a příklady uvedeme v samostatném článku). Jako hladinu významnosti určíme ɑ = 0,05. Po provedení výpočtů nám vyjde: pro pacienty užívající placebo je p-hodnota 0,092, je tedy vyšší než hladina významnosti 0,05 → placebo nesnižuje významným způsobem krevní tlak u hypertoniků, pro pacienty užívající experimentální lék p-hodnota 0,0002, která je nižší než hladina významnosti 0,05 → lék pomáhá pacientům s hypertenzí snížit vysoký krevní tlak.