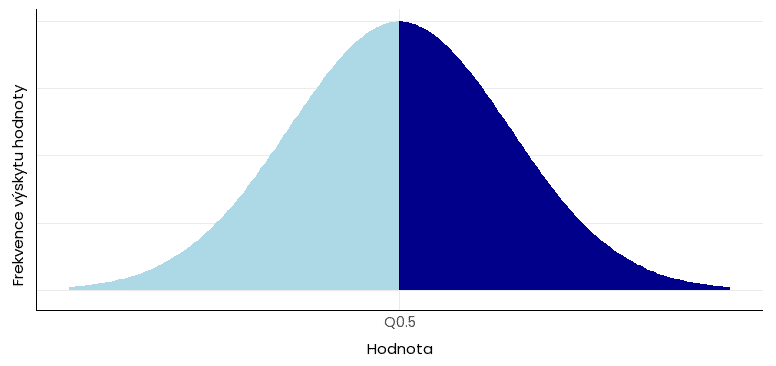
Medián je důležitým ukazatelem míry polohy. Vyjadřuje prostřední hodnotu ve vzestupně seřazeném souboru dat a dělí jej na dvě poloviny. Odděluje tedy 50 % spodních hodnot od 50 % horních hodnot.
Z tohoto pohledu jde o typ kvantilu, někdy označovaný Q0,5. Spolu s dalšími kvantily jej můžete spočítat u ordinálních proměnných a kvantitativních proměnných.
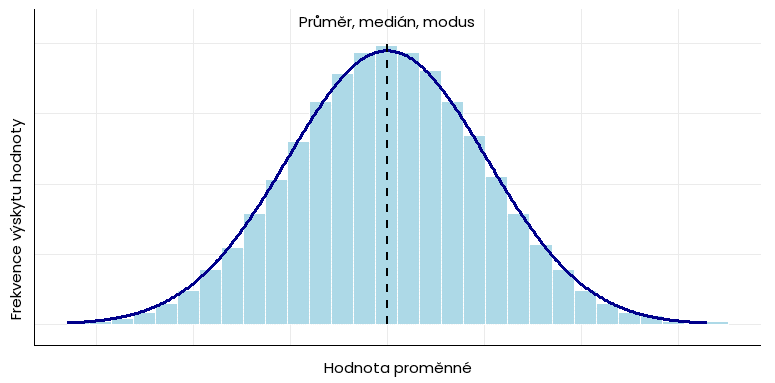
U normálního rozdělení dat se hodnota mediánu rovná hodnotě aritmetického průměru a modu:
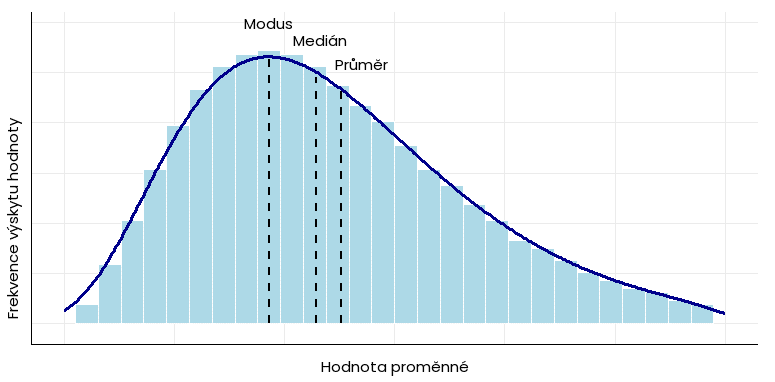
Na rozdíl od aritmetického průměru medián neovlivňují extrémní hodnoty. V jejich přítomnosti se hodnota mediánu, průměru a modu liší:
U lichého počtu hodnot se medián počítá jako prostřední hodnota seřazených dat (viz příklad níže):
V případě sudého počtu hodnot se medián rovná aritmetickému průměru dvou prostředních hodnot (viz příklad níže):

Zakupte si balíček 2 nebo více vybraných kurzů a ušetřete
V obou případech vyjadřuje \( n \) počet prvků v souboru dat, zatímco \( x_{i} \) pořadí dané hodnoty při ve vzestupném seřazeném souboru hodnot. V praxi se medián nepočítá ručně, ale s pomocí funkcí statistických programů.
Využití mediánu
Medián je obzvláště užitečný ve výzkumech a analýzách, kde je důležité identifikovat střední hodnotu datové sady, která není ovlivněna extrémními hodnotami. To z něj činí ideální nástroj např. pro hodnocení:
- příjmu v sociologických studiích, kde extrémní hodnoty (např. velmi vysoké příjmy) mohou zkreslit průměrné výsledky,
- středových hodnot v environmentálních studiích, jako je kvalita vzduchu nebo vody, kde extrémní hodnoty způsobené neobvyklými událostmi (např. znečištění) nemusí odpovídat obvyklé kvalitě,
- střední délky přežití v klinických studiích.
Kdy medián nepoužívat?
Přestože je medián užitečný v řadě aplikací, existují situace, kdy jeho použití není ideální. Jde zejména o případy, kdy:
- je potřeba zohlednit všechny hodnoty v datové sadě, včetně extrémů (např. při studiu maximální možné efektivity nebo odolnosti materiálů),
- data mají rovnoměrnou distribuci bez extrémních hodnot – střední hodnotu stejně dobře určí aritmetický průměr.
- chybí některá data (vzorec bere v potaz pořadí hodnot).
Před využitím mediánu je nezbytné určit původ odlehlých hodnot ve vašich datech. Jejich přítomnost může totiž značit i chybu v měření. Použití mediánu by v takovém případě vedlo k mylné interpretaci získaných výsledků a celé vědecké studie.
Příklad výpočtu mediánu – lichý počet hodnot
Při zkoumání průměrné délky přežití pacientů po aplikaci experimentální léčby jste u jednotlivých dobrovolníků naměřili tyto hodnoty: 22, 3, 14, 8, 12, 10, 5, 15 a 17 měsíců.
Abychom medián nalezli, hodnoty vzestupně seřadíme:
| Pořadí hodnoty | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Hodnota (měsíce) | 3 | 5 | 8 | 10 | 12 | 14 | 15 | 17 | 22 |
Máme 9 hodnot, použijeme tedy vzorec pro výpočet mediánu při lichém počtu hodnot. Po dosazení do rovnice vychází:
Medián je 5. hodnota v seřazeném souboru dat. Mediánová délka přežití (\(\tilde{x}\)) se tedy rovná 12 měsícům .
Pokud bychom u tohoto soubor spočítali aritmetický průměr, vyjde nám 11,8 měsíce. Data tedy nemají normální rozložení.
Příklad výpočtu mediánu – sudý počet hodnot
Máte za úkol vypočítat medián mzdy u následujícího (již seřazeného) souboru hodnot:
| Pořadí hodnoty | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Měsíční příjem (tisíce Kč) | 15 | 15 | 20 | 22 | 25 | 33 | 36 | 45 | 58 | 112 |
| Pořadí hodnoty | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Měsíční příjem (tisíce Kč) | 15 | 15 | 20 | 22 | 25 | 33 | 36 | 45 | 58 | 112 |
Při sudém počtu hodnot (10) dosadíme jejich počet do následujícího vzorce:
Medián mzdy je tedy 29 000 Kč, zatímco její aritmetický průměr 38 100 Kč. Rozložení dat j opět nerovnoměrné – průměr zvyšuje zejména poslední (extrémní) hodnota 112 000 Kč.
Výpočet mediánu v Excelu
# buňky A1 až A100 obsahují naměřené hodnoty
# funkce pro výpočet mediánu
=MEDIAN(A1:A100)Výpočet mediánu v jazyce R
# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)
# funkce pro výpočet mediánu
median(data)Pro hromadný výpočet mediánu a dalších charakteristik popisné statistiky v jazyce R slouží příkaz summary(), resp. describe() – podrobnosti najdete zde.



