Popisná statistika: míry variability (s příkazy pro Excel, R)

Zpracování popisných charakteristik patří mezi základní úkony při analýze dat. V minulém článku jsme řešili míry polohy, na následujících řádcích se zaměříme na míry variability. Prozkoumáme, jak (a proč) je počítat a s čím nám při statistické analýze pomohou. Nezapomeňte se podívat i na detaily o mírách četnosti a mírách tvaru.

Poznámka: pro výpočet některých měr variability a dalších popisných charakteristik v jazyce R budete potřebovat knihovnu psych, které nainstalujete a otevřete následujícím příkazem:

# instalace knihoven
install.packages(c("psych"))

Co jsou míry variability?

Míry variability popisují rozložení dat kolem průměru, mediánu či jiného středu datového souboru. Zároveň nám dávají informace o tom, jak si jsou jednotlivé hodnoty podobné (resp. jak moc se mezi sebou liší).

Mezi míry variability patří:

• rozpětí (včetně mezikvartilového),
• rozptyl,
• směrodatná odchylka,
• variační koeficient.

Jednotlivé míry variability můžete použít pouze u kvantitativních proměnných (pro kvalitativní proměnné nejsou vhodné).

Zvýhodněné balíčky kurzů

Zakupte si balíček 2 nebo více vybraných kurzů a ušetřete

Prohlédnout balíčky kurzů

Znalost měr variability (spolu s mírami polohy) je důležitá pro volbu správného typu statistické analýzy pro otestování naší alternativní hypotézy. Např. pokud:

• zjistíte, že naměřené hodnoty v souboru nemají normální rozložení (podle Gaussovy křivky), potom je třeba zvolit neparametrický test,
• naměřené hodnoty u více souboru splňují normální rozložení, ale liší se ve variabilitě, nelze např. použít t-test nebo metodu ANOVA,
• naznačuje variabilita velké množství extrémních (odlehlých) hodnot, je třeba přikročit k vhodné transformaci dat (v těchto případech se často využívá logaritmická transformace).

Obecně platí, že čím nižší variabilitu data ve vzorku vykazují, tím spíše lze vztáhnout závěry z daného výběrového souboru na celou populaci. U vysoké variability je obtížné vysledovat trend efektu studovaného jevu na určitou proměnnou.

Variační rozpětí

Rozpětí (R) je rozdíl mezi nejvyšší a nejnižší hodnotou v datové sadě. Jedná se o nejjednoduší míru variability.

Výhody: snadno se počítá, poskytuje rychlý a pochopitelný přehled o rozptýlení hodnot v sadě.

Nevýhody: rozpětí je citlivé na extrémní hodnoty a nedává nám žádné informace o struktuře dat ani jejich rozptýlení okolo středu. Jeho použití bez dalších měr variability může vést k zavádějícím interpretacím.

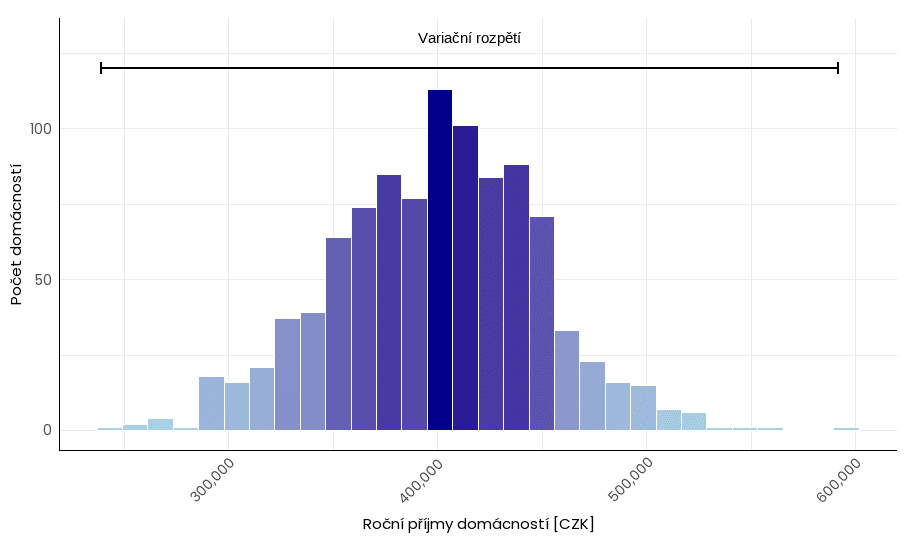
Příklad variačního rozpětí u spojité proměnné, která nabývá v určitém rozsahu libovolných hodnot (pro účely vizualizace zobrazujeme počet hodnot v rámci určitých intervalů). Všimněte si odlehlých hodnot především v pravé části grafu.

Excel: funkce pro výpočet variačního rozpětí

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet variačního rozpětí
=MAX(A1:A100) - MIN(A1:A100)

R: funkce pro výpočet variačního rozpětí

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet variačního rozpětí
max(data) - min(data)

Mezikvartilové rozpětí

Mezikvartilové rozpětí (Interquartile Range – IQR) je statistická míra variability, která vyjadřuje rozsah poloviny hodnot datové sady okolo jejího středu (typicky mediánu), tedy mezi třetím kvartilem (Q3, 75. percentil) a prvním kvartilem (Q1, 25. percentil). Počítá se jako rozdíl těchto kvartilů, tzn. IQR = Q3 – Q1.

Ve vizuálním provedení se zobrazuje tzv. box-plotem (krabicovým grafem).

Výhody: používá se k identifikaci odlehlých hodnot; jde o hodnoty, které leží mimo 1,5násobek IQR nad třetím kvartilem, resp. mimo 1,5násobek IQR pod prvním kvartilem. Zároveň informuje o variabilitě dat okolo středu datové sady.

Nevýhody: nezohledňuje variabilitu dat mimo střední polovinu hodnot.

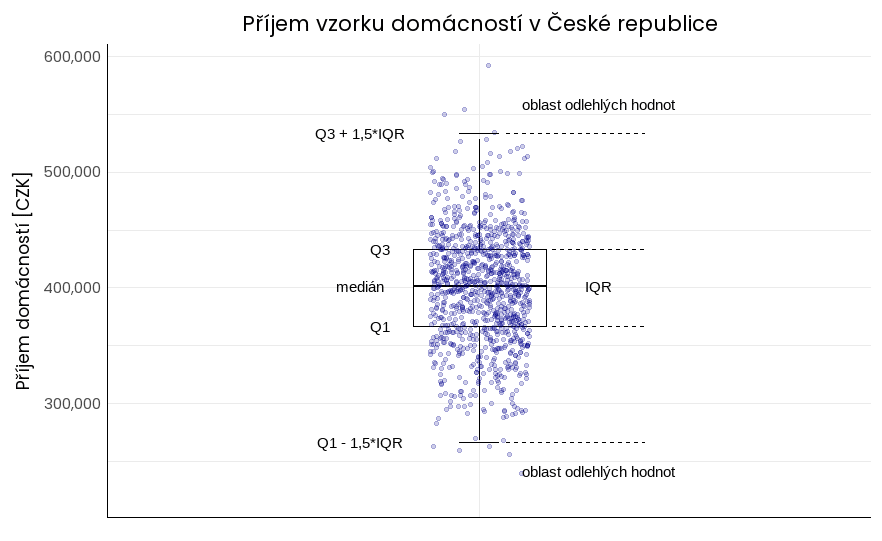
Příklad variačního rozpětí u stejné spojité proměnné jako výše. V oblasti IQR se nachází přesně polovina všech pozorování. Jedna ze zbývajících čtvrtin pozorování leží nad Q3, druhá pod Q1.

Excel: funkce pro výpočet mezikvartilového rozpětí

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet mezikvartilového rozpětí
=QUARTILE.INC(A1:A100, 3) - QUARTILE.INC(A1:A100, 1)

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet mezikvartilového rozpětí
IQR(data)

Rozptyl

Rozptyl (také disperze) udává míru rozptýlení hodnot v datovém souboru okolo jeho střední hodnoty. Tzn. čím vyšší je hodnota rozptylu, tím rozptýlenější jsou data v souboru (za předpokladu normální distribuce dat).

Hodnoty rozptylu jsou mj. důležité pro určení, zda můžeme pro otestování naší hypotézy použít metodu ANOVA a jí příbuzné testy.

V praxi rozlišujeme populační a výběrový rozptyl.

Populační rozptyl

Populační rozptyl (σ²) se počítá jako průměr kvadrátů rozdílů mezi každou hodnotou ve statistické populaci (statistickém souboru) a průměrem (střední hodnotou) této populace.

Z definice rozptylu zároveň vyplývá, že se jeho hodnota měří ve druhé mocnině měřených jednotek (např. u délky se veličina délky m změní na m²). Z tohoto důvodu je rozptyl méně intuitivní na pochopení a nelze jej přímo srovnávat s hodnotami v datovém souboru (pro tyto účely je třeba jej odmocnit – viz směrodatná odchylka níže).

Výhody: ideální pro analýzu dat celé populace (např. všech kuřáků v určitém věku a oblasti).

Nevýhody: je velmi citlivý na odlehlé hodnoty. U menšího počtu vzorků (výběrového souboru) může poskytnout zkreslené výsledky; pro použití ve statistických testech je proto vhodnější vzorkový rozptyl (viz níže).

Excel: funkce pro výpočet populačního rozptylu

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet populačního rozptylu
=VAR.P(A1:A100)

R: funkce pro výpočet populačního rozptylu

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet populačního rozptylu
var(data) * (length(data)-1)/length(data)

Výběrový rozptyl

Výběrový (vzorkový) rozptyl (s²) je odhadem populačního rozptylu z vybraného vzorku dané populace. Počítá se podobně jako populační rozptyl, ale na rozdíl od něj nevyužívá ve jmenovateli celou velikost výběrové populace (N), ale hodnotu N – 1 (tzv. počet stupňů volnosti):

Použití jmenovatele N – 1 se označuje jako Besellova oprava. Jejím účelem je – alespoň částečně – odstranit zkreslení ve výpočtu rozptylu u malého vzorku. (To je důležité, protože odlehlé hodnoty u omezeného počtu pozorování mohou výrazně zkreslit hodnotu rozptylu.) Díky tomu je pak vyšší šance, že závěry, které ze vzorku odvodíte, budou platné pro celou statistickou populaci.

Se vzorkovým rozptylem se při vyhodnocování dat setkáte mnohem častěji než s populačním a je (zpravidla) synonymem pro jednoduché označení „rozptyl“. (Výjimkou je samozřejmě situace, kdy pracujete s hodnotami proměnýnch celé statistické populace.)

Výhody: ideální pro analýzu dat výběrové populace (např. vzorku kuřáků v určitém věku a oblasti).

Nevýhody: je velmi citlivý na odlehlé hodnoty. Není vhodný pro analýzu celé populace (k tomu slouží populační rozptyl, viz výše).

Excel: funkce pro výpočet výběrového rozptylu

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet výběrového rozptylu
=VAR.S(A1:A100)

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet výběrového rozptylu
var(data)

Směrodatná odchylka

Směrodatná odchylka je jednou z nejdůležitějších (a nejpoužívanějších) měr variability. Říká nám, jak daleko se hodnoty datového souboru rozprostírají od střední hodnoty (průměru). Opět platí, že čím vyšší hodnota směrodatné odchylky, tím rozptýlenější data v souboru jsou (mají-li data v souboru normálního rozdělení).

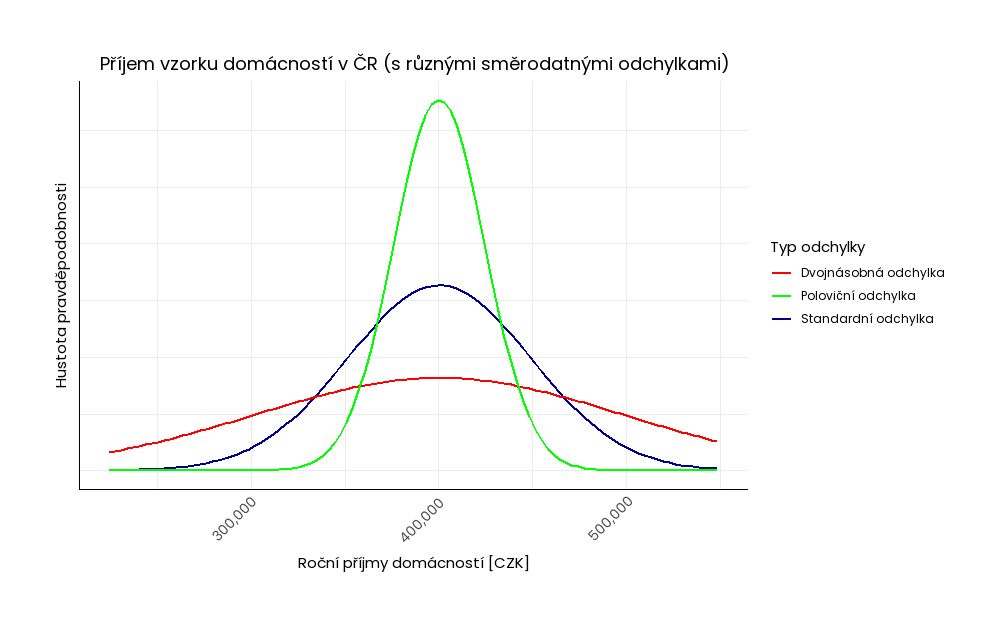
Přestože ve všech sledovaných skupinách výše dosahuje roční příjem domácností stejného průměru, u nízké hodnoty směrodatné odchylky (zelená křivka) jsou data kompaktnější a většina příjmů domácností v daném vzorku se pohybuje okolo průměru. Naopak u vysoké hodnoty směrodatné odchylky (červená křivka) jsou data v sadě více rozptýlená od středu; v tomto vzorku je tedy více nízkopříjmových a vysokopříjmových domácností.

Spolu s průměrem a mediánem dokážeme díky směrodatné odchylce odhadnout, zda je rozložení hodnot v datovém souboru normální – mj. sestavením histogramu, Q-Q grafu či P-P grafu (na toto téma připravujeme samostatný článek).

Směrodatná odchylka se počítá jako odmocnina z rozptylu. Rozlišujeme proto populační směrodatnou odchylku a vzorkovou směrodatnou odchylku.

Populační směrodatná odchylka

Populační směrodatná odchylka (σ) se počítá jako odmocnina z populačního rozptylu:

Výhody: ideální pro analýzu dat celé populace (např. všech kuřáků v určitém věku a oblasti). Je dobře pochopitelná, protože používá stejné jednotky jako naměřená data. Umožňuje posoudit konzistenci datové sady – poskytuje přehled o vzdálenosti jednotlivých hodnot od průměru.

Nevýhody: citlivá na odlehlé hodnoty. U menšího počtu vzorků (výběrového souboru) může poskytnout zkreslené výsledky; pro použití ve statistických testech je proto vhodnější vzorková směrodatná odchylka (viz níže).

Excel: funkce pro výpočet populační směrodatné odchylky

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet populační směrodatné odchylky
=STDEV.P(A1:A100)

R: funkce pro výpočet populační směrodatné odchylky

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet populační směrodatné odchylky
sqrt(var(data) * (length(data)-1)/length(data))

Výběrová směrodatná odchylka

Výběrová (vzorková) směrodatná odchylka (s) se počítá jako odmocnina ze vzorkového rozptylu. Zahrnuje v sobě tedy Besselovu opravu pro přesnější výpočet rozptylu a směrodané odchylky při omezeném počtu pozorování (viz výše):

Výhody: ideální pro analýzu dat výběrové populace (např. vzorku kuřáků v určitém věku a oblasti). Používá stejné jednotky jako naměřená data, takže je dobře pochopitelná. Zároveň vám dovoluje posoudit konzistenci datové sady – poskytuje přehled o vzdálenosti jednotlivých hodnot od průměru.

Nevýhody: citlivá na odlehlé hodnoty. Není vhodná pro analýzu celé populace (k tomu slouží populační směrodatná odchylka, viz výše).

Excel: funkce pro výpočet výběrové směrodatné odchylky

# buňky A1 až A100 obsahují naměřené hodnoty

# funkce pro výpočet populační směrodatné odchylky
=STDEV.P(A1:A100)

R: funkce pro výpočet výběrové směrodatné odchylky

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# funkce pro výpočet výběrové směrodatné odchylky
sd(data)

Variační koeficient

Variační koeficient (známý také jako koeficient variability) vyjadřuje míru variability dat v relativních jednotkách. Počítá se jako poměr směrodatné odchylky k aritmetickému průměru datové sady a vyjadřuje se v procentech.

Populační variační koeficient:

Výběrový (vzorkový) variační koeficient:

Variační koeficient využijete ke:

• zhodnocení konzistence datové sady (čím menší variační koeficient, tím vyšší konzistence a nižší rozptyl hodnot),
• srovnání variability mezi různými datovými sadami; např. v ekonomice se využívá ke srovnání volatility cen akcií. 

Výhody: snadno se počítá a umožňuje srovnání variability různě velkých souborů dat, včetně těch s odlišnými jednotkami. 

Nevýhody: nelze jej použít při nulovém nebo záporném průměru. U šikmého rozdělení dat (viz míry tvaru) a v přítomnosti odlehlých hodnot nemusí variační koeficient odrážet skutečnou míru rozdělení dat.

Excel: funkce pro výpočet variačního koeficientu

# buňky A1 až A100 obsahují naměřené hodnoty

# vzorec pro výpočet variačního koeficientu
=STDEV.S(A1:A100) / AVERAGE(A1:A100) * 100

R: funkce pro výpočet variačního koeficientu

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# vzorec pro výpočet variačního koeficientu
(sd(data) / mean(data)) * 100

Hromadný výpočet souboru popisných charakteristik v jazyce R

Pro získání základního přehledu o vlastnostech datového souboru slouží příkaz summary(), rozsáhlejší přehled získáte příkazem describe().

Příkazem summary() vypočítáte:

• minimální a maximální hodnotu datového souboru,
• hodnotu 1. a 3. kvartilu a mediánu (tedy 25., 50. a 75. percentil),
• aritmetický průměr,
• počet pozorování pro jednotlivé kategorie/úrovně (u nominálních a ordinálních proměnných).

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# výpočet souboru popisných charakteristik s funkcí summary
summary(data)

Příkazem describe() (je součástí balíčku psych, který je třeba nainstalovat a načíst) spočítáte:

• počet platných a chybějících pozorování,
• minimální a maximální hodnotu datového souboru a jeho rozsah,
• medián (50. percentil) a medián absolutních odchylek,
• aritmetický průměr a a oříznutý průměr (průměr po odstranění určitého procenta nejnižších a nejvyšších hodnot),
• směrodatnou odchylku a směrodatnou chybu průměru,
• špičatost datového souboru (rozložení hodnot v porovnání s normální distribucí),
• šikmost datového souboru.

# načtení knihovny
library(psych)

# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)

# výpočet souboru popisných charakteristik s funkcí describe
describe(data)