Aritmetický průměr je jeden z nejvyužívanějších ukazatelů popisné statistiky. Patří mezi tzv. míry polohy a vyjadřuje střední hodnotu datového souboru. U normálního rozdělení dat se hodnota aritmetického průměru rovná hodnotě mediánu.
Počítá se jako součet všech hodnot proměnné dělený celkovým počtem hodnot (viz příklad níže):
Využití aritmetického průměru
Aritmetický průměr je základem pro výpočet rozptylu a směrodatné odchylky. Hodí se pro běžná číselná data, jako je třeba výška rostlin, počet studentů nebo teplota v místnosti. Naopak není vhodný pro hodnoty:
- s odlišnou váhou (např. výpočet celkové průměru u žáků z malé a velké školy, kdy průměr velké školy má vyšší váhu – viz vážený průměr),
- vykazující určité tempo růstu či poklesu, tedy tzv. zřetězenou růstovou charakteristiku (např. průměrný roční výnos investic nebo rychlost růstu kolonie bakterií – viz geometrický průměr),
- s charakterem podílu či převrácené hodnoty (např. účinnost nebo koncentrace látky v roztoku – viz harmonický průměr).
Nevýhodou aritmetického průměru je velká citlivost na odlehlé hodnoty, které mohou významně zkreslit celkový pohled na datový soubor. Odlehlé hodnoty mohou poukazovat na chybu v měření či výběru vzorku, může jít ale také o skutečnou hodnotu, která se od ostatních výrazně liší (na téma odlehlých hodnot pro vás připravujeme samostatný článek).
Příklad výpočtu aritmetického průměru
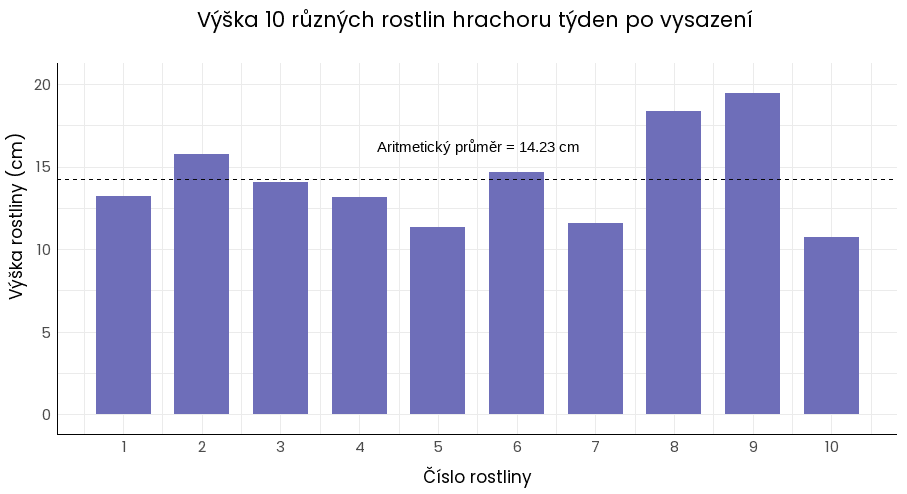
Při pozorování rychlosti růstu hrachoru jste týden po vyklíčení naměřili u 10 zástupců studovaného genotypu následující výšku (h): 10,75 cm, 11,35 cm, 11,56 cm, 13,17 cm, 13,23 cm, 14,04 cm, 14,69 cm, 15,73 cm, 18,38 cm a 19,45 cm.
Po dosazení do rovnice pro aritmetický průměr vychází:

Zakupte si balíček 2 nebo více vybraných kurzů a ušetřete
Průměrná výška rostliny po týdnu růstu je 14,23 cm.
Výpočet aritmetického průměru v Excelu
# buňky A1 až A100 obsahují naměřené hodnoty
# funkce pro výpočet aritmetického průměru
=AVERAGE(A1:A100)Výpočet aritmetického průměru v jazyce R
# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)
# funkce pro výpočet aritmetického průměru
mean(data)Pro hromadný výpočet aritmetického průměru a dalších charakteristik popisné statistiky v jazyce R slouží příkaz summary(), resp. describe() – podrobnosti najdete zde.



